Tổng hợp Công thức lượng giác lớp 11? Yêu cầu cần đạt đối với hàm số lượng giác và phương trình lượng giác môn Toán 11 là gì?

Nội dung chính

• Tổng hợp Công thức lượng giác lớp 11?
• Yêu cầu cần đạt đối với hàm số lượng giác và phương trình lượng giác tại môn Toán lớp 11 Chương trình GDPT 2018 là gì?
• Môn Toán cấp 3 Chương trình GDPT 2018 nhằm giúp học sinh đạt các mục tiêu nào?

Tổng hợp Công thức lượng giác lớp 11?

Công thức lượng giác là một kiến thức cơ bản nằm trong chương trình bộ môn toán học. Nó bao gồm các phương trình nhằm thể hiện mối liên hệ chặt chẽ với nhau giữa các hàm sin, cos, tan, cot. Sau đây là tổng hợp Công thức lượng giác lớp 11, học sinh có thể dùng để ôn tập:

[1] Công thức cộng

[2] Công thức nhân đôi

[3] Công thức biến đổi tích thành tổng

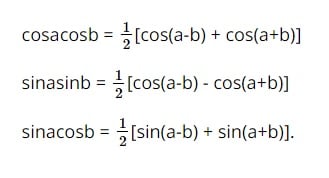
[4 ]Công thức biến đổi tổng thành tích

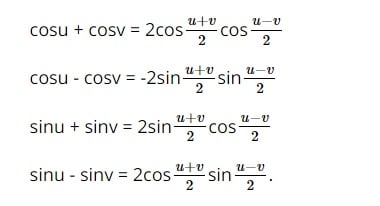
Vừa rồi là Tổng hợp Công thức lượng giác lớp 11

Tổng hợp Công thức lượng giác lớp 11? Yêu cầu cần đạt đối với hàm số lượng giác và phương trình lượng giác môn Toán 11 là gì? (Hình từ Internet)

Yêu cầu cần đạt đối với hàm số lượng giác và phương trình lượng giác tại môn Toán lớp 11 Chương trình GDPT 2018 là gì?

Căn cứ tại Nội dung chuyên đề lớp 11 Mục 5 Chương trình Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT, yêu cầu cần đạt đối với hàm số lượng giác và phương trình lượng giác tại môn Toán lớp 11 Chương trình giáo dục phổ thông 2018 như sau:

[1] Góc lượng giác. Số đo của góc lượng giác. Đường tròn lượng giác. Giá trị lượng giác của góc lượng giác, quan hệ giữa các giá trị lượng giác. Các phép biến đổi lượng giác (công thức cộng; công thức nhân đôi; công thức biến đổi tích thành tổng; công thức biến đổi tổng thành tích):

- Nhận biết được các khái niệm cơ bản về góc lượng giác: khái niệm góc lượng giác; số đo của góc lượng giác; hệ thức Chasles cho các góc lượng giác; đường tròn lượng giác.

- Nhận biết được khái niệm giá trị lượng giác của một góc lượng giác.

- Mô tả được bảng giá trị lượng giác của một số góc lượng giác thường gặp; hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác; quan hệ giữa các giá trị lượng giác của các góc lượng giác có liên quan

đặc biệt: bù nhau, phụ nhau, đối nhau, hơn kém nhau p.

- Sử dụng được máy tính cầm tay để tính giá trị lượng giác của một góc lượng giác khi biết số đo của góc đó.

- Mô tả được các phép biến đổi lượng giác cơ bản: công thức cộng; công thức góc nhân đôi; công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích.

- Giải quyết được một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác và các phép biến đổi lượng giác.

[2] Hàm số lượng giác và đồ thị

- Nhận biết được được các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.

- Nhận biết được các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.

- Nhận biết được được định nghĩa các hàm lượng giác y = sin x, y = cos x, y = tan x, y = cot x thông qua đường tròn lượng giác.

- Mô tả được bảng giá trị của bốn hàm số lượng giác đó trên một chu kì.

- Vẽ được đồ thị của các hàm số y = sin x, y = cos x, y = tan x, y = cot x.

- Giải thích được: tập xác định; tập giá trị; tính chất chẵn, lẻ; tính tuần hoàn; chu kì; khoảng đồng biến, nghịch biến của các hàm số y = sin x, y = cos x, y = tan x, y = cot x dựa vào đồ thị.

- Giải quyết được một số vấn đề thực tiễn gắn với hàm số lượng giác (ví dụ: một số bài toán có liên quan đến dao động điều hoà trong Vật lí,...).

[3] Phương trình lượng giác cơ bản:

- Nhận biết được công thức nghiệm của phương trình lượng giác cơ bản: sin x = m; cos x = m; tan x = m; cot x = m bằng cách vận dụng đồ thị hàm số lượng giác tương ứng.

- Tính được nghiệm gần đúng của phương trình lượng giác cơ bản bằng máy tính cầm tay.

- Giải được phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản (ví dụ: giải phương trình lượng giác dạng sin 2x = sin 3x, sin x = cos 3x).

- Giải quyết được một số vấn đề thực tiễn gắn với phương trình lượng giác (ví dụ: một số bài toán liên quan đến dao động điều hòa trong Vật lí,...).

Môn Toán cấp 3 Chương trình GDPT 2018 nhằm giúp học sinh đạt các mục tiêu nào?

Theo quy định Tiểu mục 4 Mục 3 Chương trình Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT, Môn Toán cấp 3 Chương trình giáo dục phổ thông 2018 nhằm giúp học sinh đạt các mục tiêu như sau:

[1] Góp phần hình thành và phát triển năng lực toán học với yêu cầu cần đạt: nêu và trả lời được câu hỏi khi lập luận, giải quyết vấn đề; sử dụng được các phương pháp lập luận, quy nạp và suy diễn để hiểu được những cách thức khác nhau trong việc giải quyết vấn đề; thiết lập được mô hình toán học để mô tả tình huống, từ đó đưa ra cách giải quyết vấn đề toán học đặt ra trong mô hình được thiết lập; thực hiện và trình bày được giải pháp giải quyết vấn đề và đánh giá được giải pháp đã thực hiện, phản ánh được giá trị của giải pháp, khái quát hoá được cho vấn đề tương tự; sử dụng được công cụ, phương tiện học toán trong học tập, khám phá và giải quyết vấn đề toán học.

[2] Có những kiến thức và kĩ năng toán học cơ bản, thiết yếu về:

- Đại số và Một số yếu tố giải tích: Tính toán và sử dụng công cụ tính toán; sử dụng ngôn ngữ và kí hiệu đại số; biến đổi biểu thức đại số và siêu việt (lượng giác, mũ, lôgarit), phương trình, hệ phương trình, bất phương trình; nhận biết các hàm số sơ cấp cơ bản (luỹ thừa, lượng giác, mũ, lôgarit); khảo sát hàm số và vẽ đồ thị hàm số bằng công cụ đạo hàm; sử dụng ngôn ngữ hàm số, đồ thị hàm số để mô tả và phân tích một số quá trình và hiện tượng trong thế giới thực; sử dụng tích phân để tính toán diện tích hình phẳng và thể tích vật thể trong không gian.

- Hình học và Đo lường: Cung cấp những kiến thức và kĩ năng (ở mức độ suy luận logic) về các quan hệ hình học và một số hình phẳng, hình khối quen thuộc; phương pháp đại số (vectơ, toạ độ) trong hình học; phát triển trí tưởng tượng không gian; giải quyết một số vấn đề thực tiễn đơn giản gắn với Hình học và Đo lường.

- Thống kê và Xác suất: Hoàn thiện khả năng thu thập, phân loại, biểu diễn, phân tích và xử lí dữ liệu thống kê; sử dụng các công cụ phân tích dữ liệu thống kê thông qua các số đặc trưng đo xu thế trung tâm và đo mức độ phân tán cho mẫu số liệu không ghép nhóm và ghép nhóm; sử dụng các quy luật thống kê trong thực tiễn; nhận biết các mô hình ngẫu nhiên, các khái niệm cơ bản của xác suất và ý nghĩa của xác suất trong thực tiễn.

[3] Góp phần giúp học sinh có những hiểu biết tương đối tổng quát về các ngành nghề gắn với môn Toán và giá trị của nó; làm cơ sở cho định hướng nghề nghiệp sau trung học phổ thông; có đủ năng lực tối thiểu để tự tìm hiểu những vấn đề liên quan đến toán học trong suốt cuộc đời.