Đường cong elliptic là gì? Quy ước trên đường cong elliptic theo TCVN 12852-1:2020 như thế nào?

Nội dung chính

• Đường cong elliptic là gì?
• Quy ước trên đường cong elliptic theo TCVN 12852-1:2020 như thế nào?
• Các tham số miền đường cong elliptic trên F(q) được quy định ra sao?

Đường cong elliptic là gì?

Căn cứ theo Tiểu mục 3.3. Mục 3 Tiêu chuẩn Việt Nam TCVN 12852-1:2020, đường cong elliptic (elliptic curve) được giải thích đường cong bậc ba E mà không có điểm kỳ dị

CHÚ THÍCH 1: Tập các điểm E cùng với một phép toán được định nghĩa một cách thích hợp (xem mục 6.2) tạo thành một nhóm abel. Trường bao gồm tất cả các hệ số của phương trình mô tả E được gọi là trường định nghĩa của E. Trong tiêu chuẩn này, chỉ các trường hữu hạn F được sử dụng làm trường xác định. Khi cần biểu thị trường định nghĩa F của E một cách rõ ràng, đường cong được ký hiệu là E/F.

CHÚ THÍCH 2: Dạng của một phương trình đường cong bậc ba sử dụng để định nghĩa một đường cong elliptic thay đổi phụ thuộc vào trường. Dạng tổng quát của một phương trình bậc ba phù hợp cho tất cả các trường hữu hạn

CHÚ THÍCH 3: Định nghĩa của một đường cong bậc ba được đưa ra trong tài liệu viện dẫn.

Đường cong elliptic là gì? Quy ước trên đường cong elliptic theo TCVN 12852-1:2020 như thế nào? (Hình từ Internet)

Quy ước trên đường cong elliptic theo TCVN 12852-1:2020 như thế nào?

Theo quy định tại Mục 6 Tiêu chuẩn Việt Nam TCVN 12852-1:2020, quy ước trên đường cong elliptic được quy định như sau:

[1] Định nghĩa các đường cong elliptic

*Đường cong elliptic trên trường F(pm)

Cho F(pm) là một trường hữu hạn với số nguyên tố p > 3 và một số nguyên dương m. Trong tiêu chuẩn này, ta giả sử rằng E được mô tả bằng một phương trình Weierstrass (dạng affine) rút gọn, tức là phương trình có dạng:

Y2 = X3 + aX + b với a, b ϵ F(pm)

Sao cho 4a3 + 27b2 ≠ 0F trong trường F(pm).

CHÚ THÍCH Đường cong trên với 4a3 + 27b2 = 0F được gọi là đường cong kỳ dị và đó không phải là một đường cong elliptic.

Tập các điểm với tọa độ trong F(pm) (các điểm F(pm) - giá trị) của E được đưa ra bởi công thức (1):

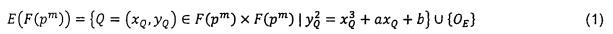
Trong đó OE là điểm đặc biệt được gọi là điểm tại vô hạn của E.

*Các đường cong elliptic trên F(2m)

Cho F(2m), với m ≥ 1 nào đó, là một trường hữu hạn. Trong tiêu chuẩn này, ta giả sử E được mô tả bởi một phương trình có dạng:

Y2 + XY = X3 + aX2 + b với a, b ϵ F(2m)

sao cho b ≠ 0F là đúng trong F(2m).

Để sử dụng trong lĩnh vực mật mã, m phải là một số nguyên tố để chống lại được các loại tấn công vào các hệ mật mã.

CHÚ THÍCH Đường cong trên với b = 0F được gọi là đường cong kỳ dị, không phải đường cong elliptic.

Tập các điểm với tọa độ trong F(2m) (các điểm F(2m) - giá trị) của E được cho bởi công thức (2)

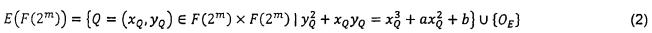
Với OE là điểm đặc biệt, được gọi là điểm tại vô hạn của E.

*Các đường cong elliptic trên trường F(3m)

Cho F(3m) là một trường hữu hạn với một số nguyên dương m. Trong tiêu chuẩn này, ta giả sử rằng E được mô tả bởi một phương trình có dạng:

Y2 = X3 + aX2 + b với a, b ϵ F(3m)

Sao cho a,b ≠ 0F trong F(3m)

CHÚ THÍCH Đường cong trên với a hoặc b = 0F được gọi là đường cong kỳ dị, không phải là đường cong elliptic.

Tập các điểm với tọa độ trong F(3m) (các điểm F(3m) - giá trị) của E được cho bởi công thức (3)

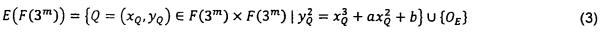
Với OE là điểm đặc biệt được gọi là điểm tại vô hạn của E.

[2] Luật nhóm trên các đường cong elliptic

Đường cong elliptic được cung cấp phép toán cộng + : E x E ® E, xác định đối với mỗi cặp {Q1,Q2} các điểm trên E một điểm thứ 3 Q1 + Q2. Với phép toán cộng này, E là một nhóm abel với phần tử trung hòa OE. Bội số k lần của Q được định nghĩa là kQ, trong đó kQ = Q + ... + Q (tổng k lần) nếu k > 0,kQ = (-k)(-Q) nếu k < 0, và kQ = OE nếu k = 0. Số dương nhỏ nhất k với kQ = OE được gọi là cấp của Q.

CHÚ THÍCH : Công thức của luật nhóm và Q được đưa ra trong B.3, B.4 và B.5

[3] Sinh các đường cong elliptic

Để sử dụng đường cong elliptic cho các hệ mật mã, việc sinh một đường cong elliptic thích hợp là cần thiết. TCVN 12852-5 là tài liệu tham chiếu cho các phương pháp sinh đường cong elliptic.

[4] Ánh xạ song tuyến tính mật mã

Ánh xạ song tuyến tính mật mã en được sử dụng trong một số ứng dụng mật mã, chẳng hạn như các lược đồ ký số hoặc lược đồ thỏa thuận khóa. Một ánh xạ song tuyến tính mật mã en được xác định qua việc lấy hạn chế trên miền xác định của các phép ghép cặp Weil hoặc Tate như sau.

en :< G1 > x < G2 > ® µn

trong đó ánh xạ song tuyến tính mật mã en thỏa mãn các tính chất sau:

- Tính song tuyến tính: en(aG1, bG2) = e(G1,G2)ab (Ɐ a,b ϵ [0, n - 1]);

- Không suy biến: en(G1, G2) ≠ 1;

- Có thể tính toán được: Tồn tại một thuật toán hiệu quả đến tính toán en.

CHÚ THÍCH 1 Mối liên hệ giữa ánh xạ song tuyến tính mật mã với phép ghép cặp Weil hoặc Tate được chỉ ra trong B.7

CHÚ THÍCH 2 Công thức cho các phép ghép cặp Weil và Tate được chỉ ra trong C.6

CHÚ THÍCH 3 Có hai kiểu ghép cặp:

- Trường hợp G1 = G2;

- Trường hợp G1 ≠ G2.

Các tham số miền đường cong elliptic trên F(q) được quy định ra sao?

Căn cứ theo Tiểu mục 8 Mục 8 Tiêu chuẩn Việt Nam TCVN 12852-1:2020, các tham số miền đường cong elliptic trên F(q) bao gồm cả các trường hợp đặc biệt F(p) và F(2m)] sẽ bao gồm các thành phần sau:

- Nếu m > 1 thì nên có một thỏa thuận về việc lựa chọn cơ sở giữa các bên tham gia liên lạc.

- Kích thước trường q = pm xác định trường hữu hạn cơ sở F(q), với p là một số nguyên tố và một chỉ dẫn rõ ràng về cơ sở được sử dụng để biểu diễn các phần tử của trường trong trường hợp m > 1;

- Nếu q = pm với p > 3, hai phần tử a và b của trường F(q) định nghĩa phương trình đường cong elliptic E: y2 + xy = x3 + ax2 + b;

- Nếu q = 2m, hai phần tử a và b của trường F(2m) định nghĩa phương trình đường cong elliptic E: y2 + xy = x3 + ax2 + b;

- Nếu q = 3m, hai phần tử a và b trong F(3m) định nghĩa phương trình đường cong elliptic E: y2 = x3 + ax2 + b;

- Hai phần tử xG và yG của trường F(q) xác định một điểm G = (xG, yG) có cấp nguyên tố trên E;

- Cấp n của điểm G:

- Đồng hệ số h = #E(F(q))/n (khi được yêu cầu bởi lược đồ cơ sở).

CHÚ THÍCH: Việc tính toán #E(F(q)) được mô tả trong tài liệu viện dẫn [4].

Trân trọng!