TIÊU
CHUẨN QUỐC GIA
TCVN
8244-1:2010
ISO
3534-1:2006
THỐNG KÊ HỌC - TỪ VỰNG - PHẦN 1: THUẬT NGỮ CHUNG VỀ THỐNG
KÊ VÀ THUẬT NGỮ DÙNG TRONG XÁC SUẤT
Statistics
- Vocabulary and symbols - Part 1: General statistical terms and terms used in
probability
Mục lục
Lời nói đầu
Lời giới thiệu
Phạm vi áp dụng
1 Thuật ngữ
chung về thống kê
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ lục A (tham khảo) Các ký hiệu
Phụ lục B (tham khảo) Sơ đồ khái niệm
về thống kê
Phụ lục C (tham khảo) Sơ đồ
khái niệm về xác suất
Phụ lục D (tham khảo) Phương pháp luận
sử dụng trong việc xây dựng từ vựng
Thư mục tài liệu tham khảo
Chỉ mục theo bảng chữ cái
Lời nói đầu
TCVN 8244-1:2010 hoàn toàn tương đương
với ISO 3534-1:2006;
TCVN 8244-1:2010 do Ban kỹ thuật Tiêu
chuẩn Quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn,
Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công
bố.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
- TCVN 8244-1:2010 (ISO 3534-1:2006),
Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
- TCVN 8244-2:2010 (ISO 3534-2:2006),
Phần 2: Thống kê ứng dụng
Bộ ISO 3534 còn có phần dưới đây có
tên chung “Statistics - Vocabulary and symbols”:
- Part 3: Design of experiments
Lời giới thiệu
Tiêu chuẩn này và TCVN 8244-2
tương thích nhau. Hai tiêu chuẩn có chung mục đích là giới hạn
mức độ toán học tương ứng đến mức tối thiểu cần thiết để có được những định
nghĩa cô đọng và chính xác. Các thuật ngữ trong Phần 1 sử dụng trong xác suất
và thống kê là các thuật ngữ cơ bản, do vậy được trình bày ở mức độ toán học
tương đối phức tạp. Thực tế là người sử dụng TCVN 8244-2 (ISO 3534-2) hoặc các
tiêu chuẩn khác về thống kê ứng dụng của TC 69 thường có thể tham khảo tiêu
chuẩn này đối với định nghĩa của các thuật ngữ nhất định, nhiều thuật
ngữ được mô tả theo cách ít thiên về kỹ thuật hơn trong nội dung chú thích và
được minh họa bằng các ví dụ. Mặc dù cách mô tả này không thay thế cho các định
nghĩa chính thức nhưng chúng có thể cung cấp định nghĩa cho các khái niệm thực tế, cho
người không có chuyên môn, do đó phục vụ cho nhu cầu của nhiều người sử dụng
các tiêu chuẩn thuật ngữ này. Nhằm hỗ trợ thêm cho người sử dụng các tiêu chuẩn
như TCVN 8244-2 (ISO 3534-2) hoặc TCVN 6910 (ISO 5725), các chú thích và ví dụ được
đưa ra làm cho tiêu chuẩn này dễ tiếp cận hơn.
Tập hợp các thuật ngữ về xác suất và
thống kê được định nghĩa đầy đủ và hoàn chỉnh rất cần thiết cho việc xây dựng
và sử dụng hiệu quả các tiêu chuẩn về thống kê. Các định nghĩa được nêu ở đây phải
đủ chính xác và phức tạp về mặt toán học nhằm giúp người xây dựng các tiêu
chuẩn về thống kê không bị nhầm lẫn. Việc giải thích chi tiết hơn các khái
niệm, ngữ cảnh và lĩnh vực ứng dụng có thể tìm trong các sách hướng dẫn về xác
suất, thống kê.
Các sơ đồ khái niệm được đưa ra trong
phụ lục tham khảo cho từng nhóm thuật ngữ: 1) thuật ngữ chung về thống kê
(trong Phụ lục B) và 2) thuật ngữ dùng trong xác suất (trong Phụ lục C). Có sáu
sơ đồ
khái
niệm đối với các thuật ngữ chung về thống kê và bốn sơ đồ cho các thuật ngữ
liên quan đến xác suất. Một số thuật ngữ xuất hiện trong nhiều sơ đồ để cho
thấy mối liên kết giữa tập hợp khái niệm này với tập hợp khái niệm khác. Phụ
lục D đưa ra giới thiệu tóm tắt về các sơ đồ khái niệm và giải thích chúng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Như một chú thích chung cho phần lớn
nội dung tiêu chuẩn, nếu không có quy định nào khác, các định nghĩa đều liên
quan đến trường hợp một chiều (một biến). Điều này được nêu ở đây nhằm tránh
việc đề cập lại nhiều lần về phạm vi một chiều cho hầu hết các định nghĩa.
THỐNG KÊ HỌC
- TỪ VỰNG VÀ KÝ HIỆU - PHẦN 1: THUẬT NGỮ CHUNG VỀ THỐNG KÊ VÀ THUẬT NGỮ DÙNG
TRONG XÁC SUẤT
Statistics -
Vocabulary and symbols - Part 1: General statistical terms and terms used in
probability
Phạm vi áp dụng
Tiêu chuẩn này quy định các thuật ngữ
chung về thống kê và thuật ngữ dùng trong xác suất được sử dụng để soạn thảo
các tiêu chuẩn khác. Ngoài ra, tiêu chuẩn này còn quy định các ký hiệu cho một
số thuật ngữ.
Các thuật ngữ được phân loại thành:
a) thuật ngữ chung về thống kê (điều
1);
b) thuật ngữ dùng trong xác suất (điều
2).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1 Thuật ngữ chung về
thống kê
1.1
Tổng thể
Toàn bộ cá thể được xem xét.
CHÚ THÍCH 1: Một tổng thể có thể là
thực và hữu hạn, thực và vô hạn hoặc hoàn toàn là giả thuyết. Đôi khi, thuật
ngữ “tổng thể hữu hạn” được sử dụng, đặc biệt là trong lấy mẫu điều tra. Tương
tự, thuật ngữ
“tổng
thể vô hạn” được sử dụng trong trường hợp lấy mẫu từ một tập không đếm được.
Trong điều 2, tổng thể được xem xét như không gian mẫu theo ngữ cảnh xác
suất (2.1).
CHÚ THÍCH 2: Tổng thể giả thuyết cho
phép tưởng tượng tính chất của dữ liệu theo nhiều giả định. Do đó, tổng thể giả
thuyết rất hữu ích ở
giai đoạn thiết kế trong các điều tra thống kê, đặc biệt để xác định cỡ
mẫu phù hợp. Tổng thể giả thuyết có thể có số lượng hữu hạn hoặc vô hạn. Khái
niệm này đặc biệt hữu ích trong
thống kê suy luận để hỗ trợ việc đánh giá độ mạnh của bằng chứng trong điều tra
thống kê.
CHÚ THÍCH 3: Hoàn cảnh nghiên cứu có
thể chỉ ra bản chất của tổng thể. Ví dụ, nếu ba ngôi làng được chọn để điều tra
nhân khẩu học hoặc sức khỏe, khi đó tổng thể bao gồm các cư dân của ba ngôi
làng cụ thể này. Một cách khác, nếu ba ngôi làng này được chọn ngẫu nhiên trong
số tất cả các làng trong một khu vực cụ thể, khi đó tổng thể sẽ gồm tất cả các
cư dân trong khu vực đó.
1.2
Đơn vị mẫu
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Tùy từng trường hợp, phần
quan tâm nhỏ nhất có thể là một cá thể, một hộ gia đình, một khu trường học,
một đơn vị hành chính, v.v...
1.3
Mẫu
Tập hợp con của tổng thể (1.1) gồm một
hoặc nhiều đơn vị mẫu (1.2)
CHÚ THÍCH 1: Đơn vị mẫu có thể là các
cá thể, các trị số hoặc thậm chí là các thực thể trừu tượng tùy thuộc vào tổng
thể nghiên cứu.
CHÚ THÍCH 2: Định nghĩa về mẫu trong
TCVN 8244- 2 (ISO 3534-2) có ví dụ về khuôn khổ lấy mẫu thiết yếu trong việc
lấy mẫu ngẫu nhiên từ một tổng thể hữu hạn.
1.4
Giá trị quan
trắc
Giá trị thu được của một tính chất gắn
với một đơn vị của mẫu (1.3).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Định nghĩa này không quy
định nguồn gốc hay cách thức thu được giá trị này. Giá trị có thể biểu diễn một
thể hiện của biến ngẫu nhiên (2.10). Ngoài ra giá trị có thể là một
trong số nhiều giá trị sẽ được phân tích thống kê sau đó. Mặc dù kết
luận đúng đòi hỏi một số cơ sở thống kê vững chắc nhưng không loại trừ việc
dùng các tính toán bằng số hoặc đồ thị bằng hình các giá trị quan trắc. Chỉ khi có
các vấn đề như xác định xác suất quan trắc một tập hợp giá trị cụ thể thì bộ
máy thống kê trở nên thích đáng và thiết yếu. Giai đoạn phân tích sơ bộ các giá
trị quan trắc thường được coi
là một phần của phân tích dữ liệu.
1.5
Thống kê mô
tả
Việc mô tả các giá trị quan trắc
(1.4) bằng đồ thị, trị số hoặc mô tả tóm tắt khác.
VÍ DỤ 1: Tóm tắt bằng số bao gồm trung bình
(1.15), độ rộng (1.10). độ lệch chuẩn mẫu (1.17), v.v...
VÍ DỤ 2: Ví dụ về tóm tắt bằng đồ thị bao gồm
biểu đồ hộp, biểu đồ, đồ thị Q-Q, đồ thị phân vị chuẩn, đám mây điểm, đám mây
điểm nhiều chiều và biểu đồ phân bố.
1.6
Mẫu ngẫu
nhiên
Mẫu (1.3) được chọn bằng
phương pháp chọn ngẫu nhiên.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Khi một mẫu gồm n
đơn vị mẫu được chọn từ không gian mẫu (2.1) hữu hạn, mỗi tổ hợp của n
đơn vị mẫu có xác suất (2.5) lấy mẫu cụ thể. Đối với phương án lấy mẫu
điều tra, xác suất riêng cho từng tổ hợp có thể được tính trước.
CHÚ THÍCH 3: Đối với việc lấy mẫu điều
tra từ một không gian mẫu hữu hạn, một mẫu ngẫu nhiên có thể được chọn bằng các
phương án lấy mẫu khác nhau như lấy mẫu ngẫu nhiên phân tầng, lấy mẫu ngẫu
nhiên hệ thống, lấy mẫu theo nhóm, lấy mẫu với xác suất lấy mẫu tỷ lệ với cỡ
biến phụ trợ và nhiều khả năng khác.
CHÚ THÍCH 4: Định nghĩa này nói chung
đề cập đến giá trị quan trắc (1.4) thực tế. Các giá trị quan trắc này
được coi là thể hiện của các biến ngẫu nhiên (2.10), trong đó mỗi giá
trị quan trắc tương ứng với một biến ngẫu nhiên. Khi hàm ước lượng
(1.12), thống kê kiểm nghiệm cho các kiểm nghiệm thống kê (1.48) hoặc khoảng
tin cậy (1.28) được suy ra từ mẫu ngẫu nhiên, thì định nghĩa này nói đến
các biến ngẫu nhiên phát sinh từ các thực thể trừu tượng chứ không phải giá trị
quan trắc thực tế của các biến ngẫu nhiên này.
CHÚ THÍCH 5: Mẫu ngẫu nhiên lấy từ
tổng thể vô hạn thường được tạo ra bởi việc lấy lặp lại từ không gian mẫu, dẫn
đến một mẫu có các biến ngẫu nhiên độc lập cùng phân bố khi áp dụng giải thích
về định nghĩa này đề cập trong Chú thích 4.
1.7
Mẫu ngẫu
nhiên đơn giản
mẫu ngẫu nhiên (1.6) của
<tổng thể hữu hạn> sao cho mỗi tập hợp con với cỡ mẫu đã cho xác suất lấy
như nhau.
CHÚ THÍCH: Định nghĩa này phù hợp với
định nghĩa nêu trong TCVN 8244-2 (ISO 3534-2), mặc dù cách diễn đạt hơi khác
nhau.
1.8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hàm số hoàn toàn xác định của các biến
ngẫu nhiên (2.10)
CHÚ THÍCH 1: Thống kê là hàm số của
các biến ngẫu nhiên trong một mẫu ngẫu nhiên (1.6) theo nghĩa nêu trong Chú
thích 4 của 1.6.
CHÚ THÍCH 2: Theo Chú thích 1, nếu {X1, X2, … Xn} là mẫu ngẫu
nhiên lấy từ phân bố chuẩn (2.50) với trung bình (2.35) μ
chưa biết và độ lệch chuẩn (2.37) σ chưa biết, khi đó (X1 + X2 + ... + Xn)/n là một thống
kê, trung bình mẫu (1.15), trong
đó [(X1 + X2 + ... + Xn)/n} - μ
không phải là thống kê vì nó có giá trị của tham số (2.9) μ chưa biết.
CHÚ THÍCH 3: Định nghĩa được nêu ở đây
là định nghĩa kỹ thuật, tương ứng với cách xử lý trong thống kế toán học.
1.9
Thống kê thứ
tự
Thống kê (1.8) xác định bởi
thứ tự của nó trong một sắp xếp không giảm của các biến ngẫu nhiên
(2.10).
VÍ DỤ: Cho các giá trị quan trắc của
một mẫu là 9, 13, 7, 6, 13, 7, 19, 6, 10, và 7. Giá trị quan trắc của các thống
kê thứ tự là 6, 6, 7, 7, 7, 9, 10, 13, 13, 19. Các giá trị này tạo thành thể
hiện của X(1) đến X(10).
CHÚ THÍCH 1: Cho giá trị quan trắc
(1.4) của một
mẫu
ngẫu nhiên
(1.6) là {x1, x2….,xn} và khi sắp
xếp
theo
thứ tự không giảm được ấn định là x(1) ≤ … ≤ x(k) ≤ …… ≤ x(n). Khi đó, (x(1)…, x(k),..., x(n)) là giá trị
quan
trắc
của thống kê thứ tự (X(1)…, X(k),..., X(n)) và x(k) là giá trị quan
trắc của thống kê thứ tự thứ k.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Thống kê thứ tự liên quan
đến các giá trị mẫu xác định bởi vị trí của chúng sau khi sắp xếp theo thứ tự không
giảm. Như trong ví dụ, có thể
dễ dàng hiểu việc
sắp xếp các giá trị mẫu (thể hiện của biến ngẫu nhiên) hơn là việc sắp xếp của
các biến ngẫu nhiên không được
quan trắc. Tuy nhiên, ta có thể hiểu về biến ngẫu nhiên từ mẫu ngẫu nhiên
(1.6) được sắp xếp theo thứ tự không giảm. Ví dụ, có thể nghiên cứu giá trị lớn
nhất trong số n biến ngẫu nhiên trước khi nhận giá trị của nó.
CHÚ THÍCH 4: Mỗi thống kê thứ tự riêng
là một thống
kê, là hàm số xác định hoàn toàn của một biến ngẫu nhiên. Hàm số này đơn giản là hàm
phân định vị trí hoặc thứ tự trong tập hợp các biến ngẫu nhiên đã được sắp xếp.
CHÚ THÍCH 5: Các giá trị
trùng lặp gây ra một vấn đề tiềm ẩn, đặc biệt đối với các biến ngẫu nhiên rời
rạc và các thể hiện có khả năng tách biệt thấp. Từ “không giảm” được sử dụng
tốt hơn từ “tăng” như một
cách tiếp cận tế nhị vấn đề này. Cần nhấn mạnh rằng các giá trị trùng lặp được duy
trì và không được gộp vào như một giá trị duy nhất. Trong ví dụ ở trên, hai thể
hiện của 6 và 6 là giá trị trùng lặp.
CHÚ THÍCH 6: Thứ tự được xác định theo
trục của đường thẳng thực và không theo giá trị tuyệt đối của các biến ngẫu
nhiên.
CHÚ THÍCH 7: Tập hợp đầy
đủ của thống kê thứ tự gồm một biến ngẫu nhiên n chiều, trong đó n
là số quan trắc trong mẫu đó.
CHÚ THÍCH 8: Các thành phần của thống
kê thứ tự cũng được coi như thống kê thứ tự nhưng với một chỉ số cho biết vị
trí của nó trong chuỗi giá trị mẫu đã được sắp xếp.
CHÚ THÍCH 9: Giá trị nhỏ nhất, lớn
nhất, và đối với cỡ mẫu số lẻ, trung vị mẫu (1.13), là trường hợp đặc
biệt của thống kê thứ tự. Ví dụ, đối với cỡ mẫu 11, X(1) là nhỏ nhất, X(11) là lớn nhất và
X(6), là trung vị
mẫu.
1.10
Độ rộng mẫu
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ: Tiếp tục với ví dụ ở 1.9, độ
rộng mẫu quan trắc là 19 - 6 = 13.
CHÚ THÍCH: Trong kiểm soát thống kê
quá trình, độ rộng mẫu thường được dùng để theo dõi độ phân tán theo thời gian
của quá trình, đặc biệt khi cỡ mẫu tương đối nhỏ.
1.11
Tâm độ rộng
trung bình (1.15) của thống
kê thứ tự (1.9) nhỏ nhất và lớn nhất
VÍ DỤ: Tâm độ rộng quan trắc của các
giá trị trong ví dụ ở 1.9 là (6+19)/2 = 12,5.
CHÚ THÍCH: Tâm độ rộng cho phép đánh
giá nhanh và đơn giản điểm giữa của các tập hợp dữ liệu nhỏ.
1.12
Hàm ước lượng
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
thống kê (1.8) dùng trong phép
ước lượng (1.36) tham số 0.
CHÚ THÍCH 1: Hàm ước lượng có thể là trung
bình mẫu (1.15) để ước lượng trung bình của tổng thể (2.35), biểu
thị bằng μ. Đối với phân bố (2.11) như phân bố chuẩn
(2.50), hàm ước lượng “tự nhiên” của trung bình tổng thể μ là trung bình
mẫu.
CHÚ THÍCH 2: Để ước lượng tính
chất của tổng thể [ví dụ mốt
(2.27) đối với một phân bố đơn biến (2.16)], một ước lượng thích hợp có
thể là hàm của (các) ước lượng của (các) tham số của phân bố hoặc có thể là hàm
phức hợp của mẫu ngẫu nhiên (1.6).
CHÚ THÍCH 3: Thuật ngữ “hàm ước lượng”
được
dùng
ở đây với nghĩa rộng. Nó bao gồm các ước lượng điểm đối với tham số, cũng như
ước lượng khoảng có thể dùng để dự đoán (đôi khi được gọi là hàm dự đoán). Hàm ước lượng
cũng có thể bao gồm các
hàm như ước lượng nhân và thống kê với mục đích đặc biệt khác. Thông tin thêm
được nêu trong chú thích của 1.36.
1.13
Trung vị mẫu
Thống kê thứ tự thứ [(n+1 )/2]
(1.9), nếu cỡ mẫu (xem TCVN 8244-2 (ISO 3534-2), 1.2.26) n là số
lẻ; tổng của thống kê thứ tự thứ (n/2) và (n/2) + 1] chia cho 2,
nếu cỡ mẫu n là chẵn.
VÍ DỤ: Tiếp theo ví dụ của
1.9, giá trị của 8 là thể hiện trung
vị mẫu. Trong trường hợp này (ngay cả cỡ mẫu bằng 10), giá trị thứ 5 và thứ 6
là 7 và 9, trung bình là 8. Trên thực tế, điều này được ghi là “trung vị mẫu là
8”, mặc dù nói một cách chặt chẽ thì trung vị mẫu được định nghĩa là biến ngẫu
nhiên.
CHÚ THÍCH 1: Đối với mẫu
ngẫu nhiên (1.6) có cỡ mẫu n, trong đó biến ngẫu nhiên (2.10)
được sắp xếp theo thứ tự không giảm từ 1 đến n, trung vị mẫu là biến ngẫu nhiên
thứ (n+1)/2 nếu cỡ mẫu là lẻ. Nếu cỡ mẫu n là chẵn thì trung vị mẫu
là trung bình của biến ngẫu nhiên thứ (n/2) và (n+1)/2.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Trung vị mẫu cung cấp hàm
ước lượng điểm giữa của phân bố, mỗi phía chứa một nửa mẫu.
CHÚ THÍCH 4: Trên thực tế, trung vị
mẫu có ích trong việc đưa ra ước lượng không nhạy với các giá trị cực trị trong
tập dữ liệu. Ví dụ, trung vị thu nhập và trung vị giá nhà ở thường được báo cáo
là giá trị tóm tắt.
1.14
Mômen mẫu bậc
k
E(Xk)
Tổng các biến ngẫu nhiên (2.10)
lũy thừa k trong mẫu ngẫu nhiên (1.6) chia cho số quan trắc trong
mẫu (1.3).
CHÚ THÍCH 1: Đối với mẫu ngẫu nhiên cỡ
n, nghĩa là {X1,
X2, …, Xn}, mômen mẫu bậc k,
E(Xk), là
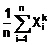
CHÚ THÍCH 2: Ngoài ra, khái niệm này
có thể được mô tả như là mômen mẫu bậc k so với điểm không.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 4: Mặc dù định nghĩa này
được đưa ra cho k bất kỳ, thường dùng trong các trường hợp thực tế k =
1 [trung bình mẫu (1.15)], k = 2 [kèm theo phương sai mẫu (1.16) và độ
lệch chuẩn mẫu (1.17)], k = 3 [liên quan đến hệ số bất đối xứng
của mẫu (1.20)] và k = 4 [liên quan đến hệ số nhọn của mẫu
(1.21)].
CHÚ THÍCH 5: “E” trong E(Xk)
lấy từ “giá trị kỳ vọng”
hoặc “kỳ vọng” của biến ngẫu nhiên X.
1.15
trung bình
mẫu
trung bình
trung bình số học
tổng các biến ngẫu nhiên (2.10)
trong mẫu ngẫu nhiên (1.6) chia
cho số các số hạng trong tổng đó.
VÍ DỤ: Tiếp theo ví dụ ở 1.9,
thể hiện của trung bình mẫu là 9,7 vì tổng các giá trị quan trắc là 97 và cỡ mẫu
là 10.
CHÚ THÍCH 1: Coi như một thống kê, trung
bình mẫu là hàm của các biến ngẫu nhiên từ mẫu ngẫu nhiên theo nghĩa nêu trong
Chú thích 3 của 1.8. Ta phải phân biệt hàm ước lượng này với trị số của trung
bình mẫu tính
được
từ các giá trị quan trắc (1.4) trong mẫu ngẫu nhiên đó.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Đối với mẫu ngẫu nhiên cỡ
n, nghĩa là {X1…, X2,.... Xn}, trung bình
mẫu là:
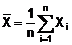
CHÚ THÍCH 4: Trung bình mẫu có thể coi
là mômen mẫu bậc 1.
CHÚ THÍCH 5: Đối với cỡ mẫu 2, trung
bình mẫu, trung vị mẫu (1.13) và tâm độ rộng (1.11) là như nhau.
1.16
Phương sai
mẫu
S2
Tổng bình phương các độ lệch của các biến
ngẫu nhiên (2.10) trong mẫu ngẫu nhiên (1.6) so với trung bình mẫu
(1.15) của chúng chia cho số các số hạng trong tổng đó trừ đi một.
VÍ DỤ: Tiếp theo ví dụ số ở 1.9, phương sai mẫu
được tính là 17,57. Tổng các bình phương của trung bình mẫu quan trắc là 158,10
và cỡ mẫu là 10 trừ đi 1 còn 9, cho mẫu số thích hợp.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Đối với mẫu ngẫu nhiên cỡ
n, nghĩa
là {X1, X2…, Xn} có trung
bình mẫu 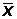 thì phương
sai
mẫu
là:
thì phương
sai
mẫu
là:
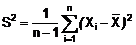
CHÚ THÍCH 3: Phương sai mẫu là một
thống kê “gần như” trung bình bình phương độ lệch của các biến ngẫu nhiên
(2.10) so với trung bình mẫu của chúng (chỉ “gần như” vì trong mẫu số n
- 1 được sử dụng thay cho n). Việc sử dụng n - 1 cung cấp
ước lượng không chệch (1.34) của phương sai (2.36) tổng thể.
CHÚ THÍCH 4: Đại lượng n - 1
được gọi là bậc tự do (2.54).
CHÚ THÍCH 5: Phương sai mẫu có thể coi
là mômen mẫu bậc hai của biến ngẫu nhiên của mẫu chuẩn hóa (1.19).
1.17
độ lệch chuẩn
mẫu
S
Căn bậc hai không âm của phương sai mẫu
(1.16).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Trên thực tế, độ lệch
chuẩn mẫu được dùng để ước lượng độ lệch chuẩn (2.37). Ở đây cũng cần
nhấn mạnh rằng S cũng là biến
ngẫu nhiên (2.10) chứ không phải là thể hiện của mẫu ngẫu nhiên (1.6).
CHÚ THÍCH 2: Độ lệch chuẩn mẫu là
thước đo độ phân tán của phân bố (2.11).
1.18
Hệ số biến
động mẫu
Độ lệch chuẩn mẫu (1.17) chia
cho trung bình mẫu (1.15).
CHÚ THÍCH: Như với hệ số biến động (2.38),
việc sử dụng thống kê này được giới hạn ở các tổng thể có giá trị dương. Hệ số
biến động thường được lấy theo phần
trăm.
1.19
Biến ngẫu
nhiên của mẫu chuẩn hóa
Biến ngẫu nhiên (2.10) trừ đi
trung bình mẫu (1.15) chia cho độ lệch chuẩn mẫu (1.17).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-0,17; 0,79; -0,64; -0,88; 0,79;
-0,64; 2,22;
-0,88;
0,07; -0,62.
CHÚ THÍCH 1: Biến ngẫu nhiên của mẫu
chuẩn hóa được phân biệt với biến ngẫu nhiên chuẩn hóa (2.33) lí thuyết tương
ứng. Mục đích của việc chuẩn hóa là để chuyển đổi thành các biến ngẫu nhiên có
trung bình “không” và độ lệch chuẩn đơn vị, để dễ dàng giải thích và so sánh.
CHÚ THÍCH 2: Giá trị quan trắc chuẩn
hóa có trung bình quan trắc bằng không và độ lệch chuẩn quan trắc bằng 1.
1.20
Hệ số bất đối
xứng của mẫu
Trung bình số học của lũy thừa bậc ba
của biến ngẫu nhiên của mẫu chuẩn hóa (1.19) từ mẫu ngẫu nhiên
(1.6).
VÍ DỤ: Tiếp theo ví dụ ở 1.9. hệ số
bất đối xứng của
mẫu
quan trắc được tính bằng 0,971 88. Với cỡ mẫu 10 trong ví dụ này, hệ số bất
đối xứng của mẫu biến động lớn, do đó phải sử dụng một cách thận trọng. Sử dụng
công thức thay thế trong Chú thích 1, tính được giá trị là 1,349 83.
CHÚ THÍCH 1: Công thức tương
ứng với định nghĩa là
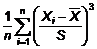
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
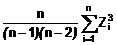
trong đó
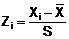
Đối với cỡ mẫu lớn, sự khác biệt giữa
hai ước lượng này là không đáng kể. Tỷ số giữa ước lượng không chệch và ước
lượng chệch là 1,389 đối với n = 10, 1,031 đối với n = 100 and
1,003 đối với n = 1 000.
CHÚ THÍCH 2: Hệ số bất đối xứng đề cập
tới sự không đối xứng. Giá trị của thống kê này gần với “không” gợi ý là phân bố đang xét
là gần đối xứng, trong khi các giá trị khác không tương ứng với phân bố khi có
các giá trị cực trị quá xa về một phía của tâm phân bố. Dữ liệu bất đối xứng cũng được
phản ánh trong các giá trị của trung bình mẫu (1.15) và trung vị mẫu
(1.13) là không giống nhau. Dữ liệu bất đối xứng dương (bất đối xứng phải) chỉ
ra khả năng có một vài
quan trắc cực trị, lớn. Tương tự, dữ liệu bất đối xứng âm (bất đối xứng trái)
chỉ ra khả năng
có một vài quan trắc cực trị, nhỏ.
CHÚ THÍCH 3: Hệ số bất đối xứng của
mẫu có thể coi là mômen mẫu bậc ba của biến ngẫu nhiên của mẫu chuẩn hóa
(1.19).
1.21
hệ số nhọn
của mẫu
trung bình số học của lũy thừa bậc bốn
của biến ngẫu nhiên của mẫu chuẩn hóa (1.19) từ mẫu ngẫu nhiên
(1.6).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Công thức tương
ứng với định nghĩa là
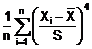
Một số bộ chương trình thống kê sử
dụng công thức dưới đây cho hệ số
nhọn của mẫu để hiệu chỉnh độ chệch (1.33) và để chỉ thị độ lệch so với
hệ số nhọn của phân bố chuẩn (bằng 3):

trong đó
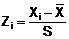
Số hạng thứ hai trong biểu thức xấp xỉ 3 đối với cỡ
mẫu n lớn. Đôi khi hệ số nhọn được lấy theo giá trị xác định ở 2.40 trừ
đi 3 để nhấn mạnh việc so sánh với phân bố chuẩn. Rõ ràng là người thực hiện
cần nhận thức được các điều chỉnh, nếu có, khi tính toán bộ chương
trình thống kê.
CHÚ THÍCH 2: Hệ số nhọn đề cập đến
tính chất nặng đuôi của một phân bố (một mốt). Đối với phân bố chuẩn
(2.50), hệ số nhọn mẫu xấp xỉ bằng 3, tùy thuộc vào độ biến động mẫu. Trên thực
tế, hệ số nhọn của phân bố chuẩn cung cấp một mốc hoặc giá trị cơ sở. Những phân
bố (2.11) có hệ số nhọn nhỏ hơn 3 có đuôi nhẹ hơn so với phân bố chuẩn, những
phân bố có hệ số nhọn lớn hơn 3 có đuôi nặng hơn phân bố chuẩn.
CHÚ THÍCH 3: Đối với các giá trị
quan trắc được của hệ số nhọn lớn hơn 3 rất nhiều, có khả năng phân bố đang xét
có đuôi nặng hơn nhiều so với phân bố chuẩn. Một khả năng khác có thể tìm ra sự
có mặt của những giá trị bất thường có thể có.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.22
Hiệp phương
sai mẫu
SXY
Tổng các tích độ lệch của cặp biến
ngẫu nhiên (2.10) trong một mẫu ngẫu nhiên (1.6) so với các trung
bình mẫu (1.15) chia cho số các số hạng trong tổng đó trừ đi một.
VÍ DỤ 1: Xét minh họa bằng số dưới đây, sử dụng
10 bộ ba giá trị quan trắc. Đối với ví dụ này, chỉ xét x và y
Bảng 1 - Kết
quả dùng cho ví dụ 1
i
1
2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4
5
6
7
8
9
10
X
38
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
24
60
41
51
58
50
65
33
y
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
74
43
107
65
73
99
72
100
48
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
34
31
40
28
35
28
32
27
27
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Trung bình mẫu quan trắc đối với X là 46,1 và đối
với
Y là 75,4. Hiệp
phương sai mẫu bằng
[(38 - 46,1) x (73 - 75,4)
+ (41 - 46,1) x (74 - 75,4)
+ ... + (33
- 46,1) x (48 - 75,4)]/9 = 257,178
VÍ DỤ 2: Trong bảng của ví dụ trên, chỉ xét y và z.
Trung bình mẫu quan trắc đối với Z là 31,3.
Hiệp phương sai mẫu bằng
[(73 - 75,4) x (34 - 31,3)
+ (74 - 75,4) x (74 - 31,3)
+ ... + (48 - 75,4) x (31 -
31,3)]/9 = -54,356
CHÚ THÍCH 1: Coi như một thống kê
(1.8), hiệp phương sai mẫu là hàm số của các cặp biến ngẫu nhiên [(X1, Y1), (X2, Y2) …, (Xn, Yn)] từ mẫu ngẫu nhiên cỡ n
theo nghĩa nêu trong Chú thích 3 của 1.6. Ước lượng (1.12) này
cần được phân biệt với trị số của hiệp phương sai mẫu tính được từ các cặp giá
trị đơn vị mẫu (1.2) quan trắc [(x1, y1), (x2,
y2), ..., (xn, yn)] trong mẫu ngẫu
nhiên. Trị số này được gọi là hiệp phương sai mẫu thực nghiệm hoặc hiệp phương
sai mẫu quan trắc.
CHÚ THÍCH 2: Hiệp phương sai mẫu SXY
được cho bằng:
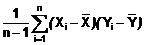
CHÚ THÍCH 3: Việc sử dụng mẫu số bằng n
- 1 cung cấp ước lượng không chệch (1.34) của hiệp phương sai tổng
thể (2.43).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.23
Hệ số tương
quan mẫu
rxy
Hiệp phương sai mẫu (1.22) chia
cho tích các độ lệch chuẩn mẫu (1.17) tương ứng.
VÍ DỤ 1: Tiếp theo Ví dụ 1 của 1.22,
độ lệch chuẩn quan trắc là 12,945 đối với X và 21,329 đối với Y.
Do đó, hệ số tương quan của mẫu quan trắc (với X và Y)
được cho bằng:
257,118/(12,948 x 21,329) = 0,931 2
VÍ DỤ 2: Tiếp theo Ví dụ 2 của 1.22,
độ lệch chuẩn quan trắc là 21,329 đối với Y và 4,165 đối với Z. Do đó, hệ
số tương quan của mẫu quan trắc (với Y và Z) được cho bằng:
-54,356/(21,329 x 4,165) =
-0,612
CHÚ THÍCH 1: Hệ số tương quan mẫu được tính theo
công thức:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Biểu thức này tương đương với tỷ số
giữa hiệp phương sai mẫu với căn bậc hai của tích các độ lệch chuẩn. Đôi khi,
kí hiệu rxy được dùng để
chỉ hệ số
tương
quan mẫu. Hệ số tương quan mẫu quan trắc dựa trên (x1, y1),
(x2, y2), …, (xn, yn).
CHÚ THÍCH 2: Hệ số tương quan mẫu quan
trắc có thể lấy giá trị trong phạm vi [-1,1], với các giá trị gần 1 chỉ ra mối
tương quan dương mạnh và các giá trị gần -1 chỉ ra mối tương quan âm mạnh. Các
giá trị gần 1 hoặc -1 chỉ ra các điểm gần như nằm trên một đường thẳng.
1.24
Sai số tiêu
chuẩn
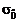
độ lệch chuẩn (2.37) của hàm
ước lượng (1.12)

VÍ DỤ: Nếu trung bình mẫu (1.15)
là ước lượng của trung bình (2.35) tổng thể và độ lệch chuẩn của một biến
ngẫu nhiên (2.10) là σ, thì sai số tiêu chuẩn của trung bình
mẫu là 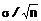 trong đó n
là số quan trắc
trong
mẫu. Ước lượng của sai số tiêu chuẩn là
trong đó n
là số quan trắc
trong
mẫu. Ước lượng của sai số tiêu chuẩn là 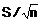 trong đó S là độ lệch
chuẩn mẫu (1.17).
trong đó S là độ lệch
chuẩn mẫu (1.17).
CHÚ THÍCH 1: Trong thực tế, sai số tiêu chuẩn cung
cấp ước lượng tự nhiên của độ lệch chuẩn của một hàm ước lượng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.25
Ước lượng
khoảng
Khoảng giới hạn bởi thống kê
(1.8) giới hạn trên và thống kê giới hạn dưới.
CHÚ THÍCH 1: Một trong các điểm cuối
có thể là +∞, -∞ hoặc giới hạn
tự nhiên của giá trị tham số. Ví dụ, 0 là giới hạn dưới của ước lượng
khoảng của phương sai (2.36) tổng thể. Trong trường hợp như vậy,
khoảng thường được đề cập là khoảng một phía.
CHÚ THÍCH 2: Ước lượng khoảng có thể
được cho cùng với ước lượng (1.36) tham số (2.9). Ước lượng
khoảng được giả định là chứa tham số theo tỷ lệ cơ hội đã định, trong điều kiện lấy
mẫu lặp lại hoặc theo nghĩa xác suất nhất định khác.
CHÚ THÍCH 3: Ba loại ước lượng khoảng
thông thường là khoảng tin cậy (1.28) đối với (các) tham số, khoảng
dự đoán (1.30) đối với các quan trắc tương lai và khoảng dung sai thống
kê (1.26) về tỷ lệ của phân bố (2.11) chứa trong đó.
1.26
Khoảng dung
sai thống kê
Khoảng xác định từ mẫu ngẫu nhiên
(1.6) sao cho với mức tin cậy quy định rằng khoảng này có thể phủ ít nhất một tỷ lệ
quy định của tổng thể (1.1) được lấy mẫu.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.27
Giới hạn dung
sai thống kê
Thống kê (1.8) biểu diễn đầu
mút của khoảng
dung
sai thống kê
(1.26)
CHÚ THÍCH: Khoảng dung sai thống kê có
thể là
- một phía (có một trong hai giới hạn cố
định ở giới hạn tự nhiên của biến ngẫu nhiên), trong đó có thể có giới hạn dung
sai thống kê trên hoặc dưới, hoặc
- hai phía, trong đó có cả hai giới
hạn dung sai thống kê.
Giới hạn tự nhiên của biến ngẫu nhiên
có thể cung cấp giới hạn cho giới hạn một phía.
1.28
Khoảng tin
cậy
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Độ tin cậy phản ánh tỷ lệ các
trường hợp khoảng tin cậy chứa giá trị tham số thực trong một loạt dải các mẫu
ngẫu nhiên (1.6) lặp lại trong các điều kiện giống nhau. Khoảng tin cậy
không phản ánh xác suất (2.5) để khoảng quan trắc chứa giá trị thực của
tham số (hoặc chứa hoặc không chứa).
CHÚ THÍCH 2: Kèm theo khoảng tin cậy là đặc
trưng hiệu năng 100(1 - α) %, trong đó α thường là một số rất nhỏ. Đặc trưng
hiệu năng, còn gọi là hệ số tin cậy hoặc mức tin cậy, thường bằng 95 % hoặc 99 %.
Bất
đẳng
thức P [T0 < θ < T1] ≥ 1 - α
đúng với giá trị θ cụ thể bất kỳ nhưng chưa biết của tổng thể.
1.29
Khoảng tin
cậy một phía
Khoảng tin cậy (1.28) có
một trong hai đầu mút cố định ở +∞, -∞, hoặc giới hạn cố định tự nhiên.
CHÚ THÍCH 1: Định nghĩa 1.28 áp dụng
với T0 đặt ở -∞
hoặc T1 đặt ở +∞.
Khoảng tin cậy một phía phát sinh trong trường hợp quan tâm tập trung vào một
phía. Ví dụ, trong kiểm tra âm lượng về an toàn liên quan đến điện thoại di
động, giới hạn tin cậy trên cần được quan tâm cho biết giới hạn trên đối với âm
lượng tạo ra trong các điều kiện an toàn giả định. Đối với phép thử kết cấu cơ
khí, giới hạn
tin cậy dưới về lực tại đó thiết bị
hỏng cần quan tâm.
CHÚ THÍCH 2: Một ví dụ khác về khoảng
tin cậy một phía là trường
hợp tham số có một giới hạn tự nhiên là “không”. Đối với phân bố Poisson (2.47) liên
quan đến xử lí khiếu nại của khách hàng thì “không” là giới hạn dưới. Trong một
ví dụ khác, khoảng tin cậy đối với độ tin cậy của linh kiện điện tử là (0,98,
1), trong đó 1 là giới hạn trên tự nhiên.
1.30
Khoảng dự
đoán
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Thông thường, quan tâm tập
trung vào một quan trắc đơn phát
sinh từ tình huống
tương tự như các quan trắc là cơ sở của khoảng dự đoán. Một huống thực tế khác
là phân tích hồi quy, trong đó khoảng dự đoán được thiết lập cho một dãy các
giá trị độc lập.
1.31
Ước lượng
Giá trị quan trắc (1.4) của
một hàm ước lượng (1.12).
CHÚ THÍCH: Ước lượng muốn nói đến trị
số thu được từ các giá trị quan trắc. Đối với phép ước lượng (1.36) của
một tham số (2.9) từ phân bố xác suất (2.11) giả thuyết, hàm ước
lượng đề cập đến thống kê (1.8) dùng để ước lượng tham số và ước lượng
đề cập đến kết quả sử dụng các giá trị quan trắc. Đôi khi, tính từ “điểm”
được đặt sau từ ước lượng để nhấn mạnh rằng một giá trị đơn được tạo ra hơn là
một khoảng các giá trị. Tương tự, tính từ khoảng được đặt sau từ ước lượng
trong trường hợp thực hiện phép ước lượng khoảng.
1.32
Sai số của
phép ước lượng
Ước lượng (1.31) trừ
đi tham số (2.9) hoặc tính chất của tổng thể dự định để ước lượng.
CHÚ THÍCH 1: Tính chất của tổng thể có
thể là hàm số của tham số hoặc các tham số hoặc đại lượng khác liên quan đến
phân bố xác suất (2.11).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.33
Độ chệch
Kỳ vọng (2.12) của sai số
của phép ước lượng (1.32)
CHÚ THÍCH 1: Định nghĩa này khác với
TCVN 8244-2 (ISO 3534-2) (3.3.2) và TCVN 6165 (VIM) (5.25 và 5.28). Ở đây độ chệch
được sử dụng theo nghĩa tổng quát như nêu trong Chú thích 1 của 1.34.
CHÚ THÍCH 2: Sự có mặt của độ chệch có
thể dẫn dến những hậu quả đáng tiếc trong thực tế. Ví dụ, việc ước lượng sai độ
bền của vật liệu có thể dẫn đến hỏng thiết bị. Trong lấy mẫu điều tra, độ chệch
có thể dẫn đến những quyết định sai của cuộc thăm dò chính trị.
1.34
Ước lượng
không chệch
Ước lượng (1.12) có độ
chệch (1.33) bằng không
VÍ DỤ 1: Đối với mẫu ngẫu nhiên
(1.6) có n biến
ngẫu nhiên (2.10) độc lập, mỗi biến có cùng
phân bố chuẩn (2.50) có trung bình (2.35) μ và độ lệch
chuẩn (2.37) σ, thì trung
bình mẫu  (1.15)
và phương sai mẫu (1.16) S2 là các ước
lượng không chệch đối với trung bình μ và phương sai (2.36) σ2,
tương ứng.
(1.15)
và phương sai mẫu (1.16) S2 là các ước
lượng không chệch đối với trung bình μ và phương sai (2.36) σ2,
tương ứng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 3: Đối với mẫu ngẫu nhiên có n cặp
biến ngẫu nhiên độc lập, mỗi cặp có cùng phân bố chuẩn hai chiều (2.65)
có hiệp phương sai (2.43) bằng ρσXY, thì hiệp
phương sai mẫu (1.22) là một ước lượng không chệch đối với hiệp phương sai
của tổng thể. Ước lượng hợp lý cực đại dùng n thay cho n - 1
trong mẫu số và do đó là
ước lượng chệch.
CHÚ THÍCH: Ước lượng không chệch
được mong muốn theo nghĩa về trung bình, chúng cho giá trị chính xác. Chắc chắn
là ước lượng không chệch cung cấp điểm bắt đầu hữu ích trong việc tìm kiếm ước lượng “tối
ưu” các tham số của tổng thể. Định nghĩa nêu ở đây là định nghĩa có tính chất thống kê.
Trong ứng dụng hàng ngày,
người thực hiện cố gắng tránh tạo ra độ
chệch cho nghiên cứu bằng cách, ví dụ, đảm bảo rằng mẫu ngẫu nhiên là đại diện
của tổng thể quan tâm.
1.35
Ước lượng hợp
lý cực đại
Ước lượng (1.12) ấn định giá
trị của tham số (2.9) tại đó hàm hợp lý (1.38)
đạt được hoặc tới gần giá trị lớn nhất của nó.
CHÚ THÍCH 1: Ước lượng hợp
lý cực đại là phương pháp tốt để thu được tham số ước lượng khi phân bố
(2.11) đã được quy định [ví dụ, phân bố chuẩn (2.50), phân
bố gamma (2.56), phân
bố Weibull (2.63),
v.v...]. Các hàm ước lượng này có tính chát thống kê mong muốn (ví dụ, phép
biến đổi đơn điệu) và trong nhiều trường hợp cung cấp phương pháp chọn phép ước
lượng. Trong các trường hợp hàm ước lượng hợp lý cực đại là chệch, đôi khi có
sự hiệu chính đơn giản độ chệch (1.33). Như đề cập trong ví dụ 2 của
1.34, ước lượng hợp lý cực đại đối với phương sai (2.36) của phân bố
chuẩn là ước lượng chệch nhưng có thể hiệu chỉnh bằng cách sử dụng n - 1
thay cho n. Phạm vi độ chệch trong những trường hợp như vậy giảm khi cỡ
mẫu tăng.
CHÚ THÍCH 2: Từ viết tắt MLE thưởng
được sử dụng cho cả hàm ước lượng hợp lý cực đại và phép ước lượng hợp lý cực
đại với ngữ cảnh chỉ ra sự lựa chọn thích hợp.
1.36
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Quy trình thu được đại diện thống kê
của tổng thể (1.1) từ mẫu ngẫu nhiên (1.6) lấy từ tổng thể này.
CHÚ THÍCH 1: Đặc biệt, quy trình này
liên quan đến tiến trình từ một hàm ước lượng (1.12) đến một ước
lượng cụ thể (1.31) cấu thành phép
ước lượng.
CHÚ THÍCH 2: Phép ước lượng được hiểu
theo nghĩa rộng hơn để bao gồm cả ước lượng điểm, ước lượng khoảng hoặc ước
lượng tính chất của tổng
thể.
CHÚ THÍCH 3. Thông thường, đại diện
thống kê đề cập đến phép ước lượng một tham số (2.9) hoặc các tham số
hoặc hàm của tham số từ một mô hình giả định. Tổng quát hơn, đại
diện của tổng thể có thể ít cụ thể hơn, ví dụ như các thống kê liên quan đến
tác động của các thảm họa tự nhiên (chết, bị thương, mất tài sản và tổn thất về
nông nghiệp - tất cả những điều
mà nhà quản lý tình trạng khẩn cấp mong muốn
ước lượng).
CHÚ THÍCH 4: Việc xem xét thống kê
mô tả (1.5) có thể gợi ý rằng mô hình giả định cung cấp đại diện
không đầy đủ các dữ liệu,
như được chỉ ra nhờ thước đo sự phù hợp của mô hình đó đối với các dữ liệu.
Trong trường hợp như vậy, cần xem xét các mô hình khác và quá trình ước lượng
được tiếp tục.
1.37
Phép ước
lượng hợp lý cực đại
Phép ước lượng (1.36) dựa
trên hàm ước lượng hợp lý cực đại (1.35)
CHÚ THÍCH 1: Đối với phân bố chuẩn
(2.50), trung bình mẫu (1.15) là hàm ước lượng hợp lý cực đại
(1.35) của tham số (2.9) μ trong khi phương sai mẫu (1.16), sử
dụng mẫu số n thay cho là n -1, cung cấp hàm ước lượng hợp lý cực
đại σ2. Mẫu số
n - 1 thường được dùng vì giá trị này
cung cấp ước lượng không chệch (1.34).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Mặc dù trong một số
trường hợp, cho ra biểu thức dạng hiền việc sử dụng phép ước lượng hợp lý cực đại
tường minh, nhưng vẫn có các trường hợp khác, trong đó hàm ước lượng hợp lý cực đại
đòi hỏi việc giải lặp đối với một tập hợp các phương trình.
CHÚ THÍCH 4: Từ viết tắt MLE thường
được sử dụng cho cả hàm ước lượng
hợp lý cực đại và phép ước lượng hợp lý cực đại theo ngữ cảnh chỉ ra sự lựa chọn
thích hợp.
1.38
Hàm hợp lý
Hàm mật độ xác suất (2.26) đánh
giá tại các giá trị quan trắc (1.4) và được coi là hàm số của các tham
số (2.9) của họ phân bố (2.8) đó.
VÍ DỤ 1: Xét trường hợp
mười cá thể được chọn ngẫu nhiên từ một tổng thể (1.1) rất lớn và 3
trong số đó có đặc trưng
riêng. Từ mẫu này, ước lượng (1.31) trực giác của tỷ lệ tổng thể có đặc
trưng là 0,3 (3 trong số 10). Trong mô hình phân bố nhị phân (2.46), hàm xác
suất (hàm khối lượng xác suất như hàm của p với n cố định tại 10 và x tại 3) đạt
giá trị lớn nhất tại p = 0,3, vì vậy thống nhất với trực giác.
[Điều này có thể xác nhận thêm bằng cách vẽ
hàm khối lượng xác suất của phân bố nhị phân (2.46) 120 p3 (1 - p)7 theo p).]
VÍ DỤ 2: Đối với phân bố chuẩn
(2.50) đã biết độ lệch chuẩn (2.37), nói chung có thể chứng tỏ rằng hàm
xác suất có giá trị lớn nhất tại μ bằng trung bình mẫu.
1.39
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hàm xác suất (1.38) như hàm của
một tham số (2.9) duy nhất với tất cả các tham số khác được đặt để
hàm đó đạt cực đại
1.40
Giả thuyết
H
Nhận định về tổng thể (1.1).
CHÚ THÍCH: Thông thường, nhận định về
tổng thể liên quan đến một hoặc nhiều tham số (2.9) trong một họ phân bố
(2.8) hoặc về họ phân bố đó.
1.41
Giả thuyết
không
H0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 1: Trong một mẫu ngẫu nhiên
(1.6) các biến ngẫu nhiên (2.10) độc lập có cùng phân bố chuẩn (2.50) với trung
bình (2.35) và độ lệch chuẩn (2.37) chưa biết, giả thuyết không đối
với trung bình μ có thể là trung bình này nhỏ hơn hoặc bằng giá trị μ0 đã cho và
điều này thường được viết theo cách sau: H0: μ ≤ μ0.
VÍ DỤ 2: Giả thuyết không có thể là mô
hình thống kê đối với một tổng thể (1.1) là phân bố chuẩn. Đối với loại giả thuyết không
này, trung bình và độ lệch chuẩn không được cho trước.
VÍ DỤ 3: Giả thuyết không có thể là mô
hình thống kê
đối với tổng thể gồm phân bố đối xứng. Đối với loại giả thuyết không này, dạng phân
bố không được cho trước.
CHÚ THÍCH 1: Rõ ràng là giả thuyết
không có thể bao gồm một tập con từ một tập hợp các phân bố xác suất có thể.
CHÚ THÍCH 2: Định nghĩa này không nên
coi là tách biệt với đối giả thuyết (1.42) và phép kiểm nghiệm thống
kê (1.48), vì việc áp dụng đúng kiểm nghiệm giả thuyết đòi hỏi tất cả các
thành phần này.
CHÚ THÍCH 3: Trong thực tế, ta không
bao giờ chứng minh giả thuyết không nhưng việc đánh giá trong tình huống đặt
ra có thể không thỏa đáng để bác bỏ giả thuyết không. Động cơ ban đầu của việc tiến
hành kiểm nghiệm giả thuyết bắt nguồn từ mong muốn rằng kết luận sẽ nghiêng về
đối giả thuyết cụ thể liên quan đến vấn đề được xét.
CHÚ THÍCH 4: Việc không bác bỏ giả
thuyết không không phải là “chứng minh” về hiệu lực của nó mà có thể chỉ ra rằng
không có đủ bằng chứng để phản bác. Hoặc giả thuyết không (hoặc gần giống) thực
tế là
đúng
hoặc cỡ mẫu không đủ để phát hiện
sự khác biệt so với giả thuyết.
CHÚ THÍCH 5: Trong nhiều tình huống,
quan tâm ban đầu tập trung vào giả thuyết không nhưng khả năng sai khác cũng có
thể được quan tâm. Sự xem xét thích hợp cỡ mẫu và hiệu lực trong việc phát hiện
sai lệch hoặc thay đổi cụ thể có thể dẫn đến việc thiết lập một quy trình kiểm
nghiệm để đánh giá một cách thích hợp giả thuyết không.
CHÚ THÍCH 6: Việc chấp nhận đối giả
thuyết trái ngược với việc không bác bỏ giả thuyết không là một kết quả tích
cực ở chỗ nó hỗ trợ mối quan tâm phỏng đoán. Việc bác bỏ giả thuyết không, ủng hộ đối
giả thuyết là kết quả rõ ràng hơn kết quả như “không bác bỏ giả thuyết không
tại thời điểm này”.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 8: Giả thuyết không thường
được biểu thị là H0.
CHÚ THÍCH 9: Nếu có thể, tập con nhận
biết giả thuyết không cần được chọn sao cho nhận định không phù hợp với phỏng
đoán cần nghiên cứu. Xem chú thích 2 của 1.48 và ví dụ trong 1.49.
1.42
Đối giả
thuyết
HA, H1
Nhận định chọn một tập hợp hoặc một
tập con tất cả các phân bố xác suất (2.11) có thể chấp nhận được không
nằm trong giả thuyết không (1.41).
VÍ DỤ 1: Đối giả thuyết của giả thuyết
không nêu trong ví dụ 1 của 1.41 là trung bình (2.35) lớn hơn giá trị
quy định, được viết theo cách sau: HA: μ > μ0.
VÍ DỤ 2: Đối giả thuyết của giả thuyết không
nêu
trong
ví dụ 2 của 1.41 là mô hình thống kê của tổng thể không phải là phân bố chuẩn
(2.50).
VÍ DỤ 3: Đối giả thuyết của giả thuyết
không nêu trong ví dụ 3 của 1.41 là mô hình thống kê của tổng thể gồm một phân
bố không đối xứng. Đối với đối giả thuyết này, dạng không đối xứng cụ thể không
được quy định.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Đối giả thuyết có thể
được biểu thị bằng H1 hoặc HA mà không có sự
ưu tiên rõ ràng miễn là cách kí hiệu tương đương với kí hiệu của giả thuyết không.
CHÚ THÍCH 3: Đối giả thuyết là nhận
định trái ngược với giả thuyết không. Thống kê kiểm nghiệm (1.52) tương
ứng được dùng để quyết định giữa giả thuyết không và đối giả thuyết.
CHÚ THÍCH 4: Không nên tách biệt đối
giả thuyết với giả thuyết không cũng như phép kiểm nghiệm thống kê
(1.48).
CHÚ THÍCH 5: Việc chấp nhận đối giả
thuyết trái với việc không bác bỏ giả thuyết không là một kết quả tích cực ở
chỗ nó hỗ trợ mối quan tâm phỏng đoán.
1.43
Giả thuyết
đơn
Giả thuyết (1.40) quy định một
phân bố duy nhất trong một họ phân bố (2.8).
CHÚ THÍCH 1: Giả thuyết đơn là giả
thuyết không (1.41) hoặc đối giả thuyết (1.42)
trong đó tập con được chọn chỉ gồm một phân bố xác suất (2.11) duy
nhất.
CHÚ THÍCH 2: Trong một mẫu ngẫu
nhiên (1.6) các biến ngẫu nhiên (2.10) độc lập có cùng phân bố
chuẩn (2.50) với trung bình (2.35) chưa biết và độ lệch chuẩn (2.37) σ
đã biết, giả thuyết đơn đối với trung bình μ là trung bình bằng giá trị μ0 đã cho và điều
này thường được viết như sau: H0: μ = μ0.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.44
Giả thuyết
hợp
Giả thuyết (1.40) quy định
nhiều hơn một phân bố (2.11) trong một họ phân bố (2.8).
VÍ DỤ 1: Giả thuyết không (1.41)
và đối giả thuyết (1.42) nêu trong ví dụ ở 1.41 và 1.42 đều là ví dụ của
giả thuyết hợp.
VÍ DỤ 2: Trong 1.48, giả thuyết không
trong Trường hợp 3 của Ví dụ 3 là một giả thuyết đơn. Giả thuyết không trong Ví
dụ 4 cũng là một giả thuyết đơn. Các giả thuyết khác trong 1.48 là giả thuyết
hợp.
CHÚ THÍCH: Giả thuyết hợp là một giả thuyết không
hoặc đối giả thuyết trong đó tập con được chọn gồm nhiều phân bố xác suất.
1.45
Mức ý nghĩa
α
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Nếu giả thuyết không là một
giả thuyết đơn (1.43), thì xác suất bác bỏ giả thuyết không khi nó đúng
sẽ là một giá trị duy nhất.
1.46
Sai lầm loại
I
Bác bỏ giả thuyết không (1.41) trong
khi trên thực tế giả thuyết không là đúng.
CHÚ THÍCH 1: Trong thực tế, sai lầm
loại I là một
quyết
định sai. Do đó, ta mong muốn
duy trì xác suất (2.5) đưa ra quyết định sai như vậy càng nhỏ càng tốt. Để
đạt được xác suất bằng
không sai lầm loại I, ta có thể không bao giờ bác bỏ giả thuyết không. Nói cách
khác là không quan tâm đến bằng chứng khi đưa ra quyết định.
CHÚ THÍCH 2: Có khả năng trong một số
tình huống (ví dụ, phép kiểm nghiệm tham số nhị phân p), mức ý nghĩa quy
định trước 0,05 là không thể đạt được do sự rời rạc của các kết quả.
1.47
Sai lầm loại
II
Việc không bác bỏ giả
thuyết không (1.41) trong khi trên thực tế giả
thuyết không không đúng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.48
Phép kiểm
nghiệm thống kê
Kiểm nghiệm mức ý nghĩa
Quy trình quyết định xem liệu có bác
bỏ giả thuyết không (1.41) và chấp nhận đối giả thuyết (1.42) hay không.
VÍ DỤ 1: Nếu một biến
ngẫu nhiên liên tục (2.29) thực tế có thể lấy giá trị từ -∞ đến +∞ và có nghi
ngờ rằng phân bố xác suất thực không phải là phân bố chuẩn (2.50), thì
các giả thuyết sẽ được lặp như dưới đây.
- Phạm vi của trường hợp này là tất cả các phân
bố xác suất liên tục
(2.23), có thể lấy giá trị từ -∞ đến +∞.
- Phỏng đoán là phân bố xác suất thực
không phải là phân bố chuẩn.
- Giả thuyết không là phân bố xác suất
là phân bố chuẩn.
- Đối giả thuyết là phân bố xác suất
không phải là phân bố chuẩn.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 3: Ví dụ này xem xét ba khả năng
trong phép kiểm nghiệm thống kê.
Trường hợp 1. Phỏng đoán rằng trung
bình quá trình cao hơn trung bình mục tiêu của μ0. Phỏng đoán
này dẫn đến các giả thuyết sau:
Giả thuyết không: H0: μ ≤ μ0
Đối giả thuyết: H1: μ
> μ0
Trường hợp 2. Phỏng đoán rằng trung
bình quá trình thấp hơn trung bình mục tiêu của μ0. Phỏng đoán này
dẫn đến các giả thuyết sau:
Giả thuyết không: H0: μ ≥ μ0
Đối giả thuyết: H1: μ < μ0
Trường hợp 3. Phỏng đoán rằng trung
bình quá trình không bằng trung bình quá trình nhưng không quy định hướng.
Phỏng đoán này dẫn đến các giả thuyết sau:
Giả thuyết không: H0: μ = μ0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Trong cả ba trường hợp, việc thiết lập
các giả thuyết đều bắt nguồn từ phỏng đoán liên quan đến đối giả thuyết và sự
sai lệch của đối giả thuyết so với điều kiện cơ sở.
VÍ DỤ 4: Ví dụ này xét trong phạm vi
tất cả các tỷ lệ
khuyết tật trong hai lô 1 và 2, p1 và p2 nhận các giá
trị từ không đến một. Ta có thể
nghi ngờ rằng hai lô là khác nhau và do đó phỏng đoán rằng tỷ lệ
khuyết tật trong hai lô là khác nhau. Phỏng đoán này dẫn đến các giả thuyết
sau:
Giả thuyết không: H0: p1 =
p2
Đối giả thuyết: H1: p1 ≠ p2
CHÚ THÍCH 1: Phép kiểm nghiệm thống kê
là một quy trình, đúng trong những điều kiện quy định, để quyết định
việc phân bố xác suất
thực tuân theo giả thuyết không hay đối giả thuyết, dựa vào các quan trắc trên
mẫu.
CHÚ THÍCH 2: Trước khi tiến hành phép
kiểm nghiệm thống kê, tập hợp các phân bố xác suất được xác định trước trên cơ sở thông tin có
sẵn. Tiếp đó, các phân bố xác suất, có thể đúng trên cơ sở
phỏng đoán cần nghiên cứu, được nhận biết để thiết lập đối giả thuyết. Sau
cùng, lập nên giả thuyết không để bổ sung cho đối giả thuyết. Trong nhiều
trường hợp, tập hợp có thể của các phân bố xác suất và từ đó giả
thuyết không và đối giả thuyết cũng có thể được xác định bằng cách tham chiếu
các tập hợp giá trị của các tham số liên quan.
CHÚ THÍCH 3: Vì quyết định dựa trên cơ
sở các quan trắc mẫu nên có thể dẫn đến sai lầm
loại I
(1.46), bác bỏ giả thuyết không trong khi giả thuyết không là đúng, hoặc sai
lầm loại II (1.47),
không bác bỏ giả thuyết không ủng hộ đối giả thuyết trong khi đối giả thuyết là đúng.
CHÚ THÍCH 4: Trường hợp 1 và 2 trong
ví dụ 3 ở trên là ví dụ về phép kiểm nghiệm một phía. Trường hợp 3 là ví
dụ về phép kiểm nghiệm hai phía. Trong cả ba trường hợp, lựa chọn một phía hay hai
phía được xác định bằng việc xem xét vùng tham số μ tương ứng với
đối giả thuyết. Tổng quát hơn, phép
kiểm nghiệm một phía và hai phía có thể bị chi phối bởi vùng bác bỏ giả thuyết
không ứng với thống kê kiểm nghiệm đã chọn. Nghĩa là, thống kê kiểm nghiệm có
một vùng tới hạn thuận cho đối giả thuyết, nhưng nó có thể không liên quan trực
tiếp đến mô tả đơn giản không gian tham số như trong các trường hợp 1, 2 và 3.
CHÚ THÍCH 5: Cần thận trọng
đối với việc đưa ra các giả định cơ bản hoặc việc ứng dụng sai phép kiểm nghiệm thống
kê. Phép kiểm nghiệm thống kê dẫn đến những kết luận ổn định ngay cả
trong trường hợp quy định sai của các giả định cơ bản được gọi là ổn định.
Phép kiểm nghiệm t một mẫu đối với trung bình là một ví dụ về phép kiểm
nghiệm được coi là rất ổn định ở các phân bố không chuẩn. Phép kiểm nghiệm
Bartlett đối với tính thuần nhất của các phương sai là một ví dụ về quy trình
không ổn định, có khả năng dẫn đến
việc bác bỏ quá mức sự bằng nhau của các phương sai trong các trường hợp phân bổ trong đó
các phương sai trên thực tế là như nhau.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
p-giá trị
xác suất (2.5) quan trắc thấy
giá trị thống kê kiểm nghiệm (1.52) được quan trắc hoặc giá trị khác bất
kỳ ít nhất là không thuận cho giả thuyết không (1.41).
VÍ DỤ: Xét ví dụ số ban đầu nêu trong
1.9. Giả sử để minh họa rằng các giá trị này là giá trị quan trắc từ quá trình mà
thông thường mong muốn có trung bình là 12,5, từ kinh nghiệm trước đó, người kỹ
sư cùng với quá trình cảm thấy rằng quá trình này thấp hơn giá trị mong muốn
trên. Một nghiên cứu được thực hiện và một mẫu ngẫu nhiên cỡ mẫu 10 được chọn
với các kết quả số ở 1.9. Các giả thuyết thích hợp là:
Giả thuyết không: H0:
μ ≥ 12,5
Đối giả thuyết: H0: μ <12,5
Trung bình mẫu là 9,7 theo hướng của
phỏng đoán nhưng có
đủ
cách
xa 12,5 để hỗ trợ phỏng
đoán hay không? Đối với ví dụ này thống kê kiểm nghiệm (1.52) là -1,976
4 với p-giá trị tương ứng 0,040. Điều này có nghĩa là có ít hơn bốn cơ
hội trong một trăm quan trắc giá trị thống kê kiểm nghiệm là -1,976 4 hoặc thấp
hơn, nếu trong thực tế trung bình thực của quá trình là 12,5. Nếu mức ý nghĩa
quy định trước ban đầu là 0,05, thì thông thường ta sẽ bác bỏ giả thuyết không
và chấp nhận đối giả thuyết.
Giả sử khác là vấn đề được
trình bày hơi khác đôi chút. Hình dung là vấn đề liên quan là quá
trình chệch khỏi mục tiêu 12,5 nhưng hướng không được xác định. Điều này dẫn
đến các giả thuyết sau:
Giả thuyết không: H0:
μ ≈ 12,5
Đối giả thuyết: H1: μ ≠ 12,5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Nếu p-giá trị, ví dụ, trở
thành 0,029, thì theo giả thuyết không, sẽ có ít hơn ba cơ hội trên một trăm
lần xuất hiện cực trị của thống kê kiểm nghiệm hoặc vượt quá cực trị. Dựa vào thông tin
này, ta có thể buộc phải bác bỏ giả thuyết không vì đó là một
p-giá trị
tương đối nhỏ. Chính thức hơn thì nếu mức ý nghĩa được đặt là 0,05, thì rõ ràng
p-giá trị là 0,029 nhỏ hơn 0,05 dẫn đến việc bác bỏ giả thuyết không.
CHÚ THÍCH 2: Thuật ngữ p-giá trị đôi
khi được gọi là xác suất ý nghĩa mà không nên nhầm với mức ý nghĩa
(1.45) là một hằng số quy định trong một ứng dụng.
1.50
Hiệu lực của
phép kiểm nghiệm
Một trừ đi xác suất (2.5) mắc sai
lầm loại II (1.47).
CHÚ THÍCH 1: Hiệu lực của phép kiểm
nghiệm đối
với
một giá trị quy định của một tham số (2.9) chưa biết trong một họ
phân bố (2.8) bằng xác suất bác bỏ giả thuyết không (1.41)
đối với giá trị tham số đó.
CHÚ THÍCH 2: Trong hầu hết các trường
hợp thực tế, việc tăng cỡ
mẫu sẽ làm tăng hiệu lực của phép kiểm nghiệm. Nói cách khác là xác suất bác bỏ
giả thuyết không khi đối giả thuyết (1.42) là đúng sẽ tăng khi cỡ mẫu
tăng, từ đó làm giảm xác
suất sai lầm loại II.
CHÚ THÍCH 3: Các trường hợp kiểm
nghiệm thường mong muốn khi cỡ mẫu trở nên cực lớn, thậm chí sai lệch nhỏ so
với giả thuyết không phải được phát hiện, dẫn tới bác bỏ giả thuyết không. Nói
cách khác, hiệu lực của phép kiểm nghiệm cần đạt đến 1 đối với từng đối giả
thuyết của giả thuyết không khi cỡ mẫu lớn đến vô cùng. Phép kiểm nghiệm như
vậy gọi là nhất quán. Khi
so sánh hai phép kiểm nghiệm về hiệu lực, phép kiểm nghiệm có hiệu lực cao hơn
có vẻ có hiệu quả hơn với điều kiện các mức ý nghĩa giống nhau cũng như các giả
thuyết không và đối giả thuyết. Có các mô tả toán học chính thức hơn cho cả tính nhất
quán và hiệu quả không thuộc phạm vi của tiêu chuẩn này. (Tham khảo các sách thống kê
hoặc sách toán thống kê.)
1.51
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Tập hợp các giá trị hiệu lực của
phép kiểm nghiệm (1.50) là hàm số của tham số (2.9) tổng thể từ một họ
phân bố (2.8).
CHÚ THÍCH: Hàm hiệu lực bằng một trừ
đi đường hiệu quả.
1.52
Thống kê kiểm
nghiệm
Thống kê (1.8) sử dụng cùng
với phép kiểm nghiệm thống kê (1.48)
CHÚ THÍCH: Thống kê kiểm nghiệm được
dùng để đánh
giá phân bố xác suất (2.11) được xét có phù hợp với giả
thuyết không (1.41) hoặc đối giả thuyết (1.42) hay không.
1.53
Thống kê mô
tả đồ thị
Thống kê mô tả (1.5) dưới
dạng hình ảnh.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.54
Thống kê mô
tả dạng số
Thống kê mô tả (1.5) dưới
dạng số.
CHÚ THÍCH: Thống kê mô tả bằng số bao
gồm trung bình (1.15), độ rộng mẫu (1.10), độ lệch chuẩn mẫu
(1.17), độ rộng giữa các tứ phân vị,...
1.55
Các lớp
CHÚ THÍCH: Các lớp được giả định là
đầy đủ và loại trừ lẫn nhau. Đường thẳng thực là tất cả các số thực nằm
trong khoảng từ -∞ đến +∞.
1.55.1
Lớp
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.55.2
Lớp
<đặc trưng thứ tự> Tập hợp một
hoặc nhiều loại được sắp xếp theo một thang thứ tự.
1.55.3
Lớp
<đặc trưng định lượng>
Khoảng của đường thẳng thực.
1.56
Giới hạn lớp
Biên giới lớp
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Định nghĩa này đề cập đến
giới hạn lớp kèm theo đặc trưng định lượng.
1.57
Điểm giữa lớp
<đặc trưng định lượng> Trung
bình (1.15) giữa giới hạn lớp (1.56) trên và dưới.
1.58
Độ rộng lớp
<đặc trưng định lượng> Giới hạn
trên của lớp trừ đi giới hạn dưới của lớp (1.55).
1.59
Tần số
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.60
Phân bố tần
số
Mối quan hệ theo thực nghiệm giữa các lớp
(1.55) và số lần xuất hiện của chúng hoặc giá trị quan trắc (1.4).
1.61
Biểu đồ phân
bố
Cách biểu diễn phân bố tần số
(1.60) bằng đồ thị gồm các hình chữ nhật liền nhau, mỗi hình có độ rộng bằng
với độ rộng lớp (1.58) và diện tích tỷ lệ với tần số lớp.
CHÚ THÍCH: Cần chú ý đối
với trường hợp dữ liệu trong các lớp có độ rộng lớp không bằng nhau.
1.62
Biểu đồ cột
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Các hình chữ nhật đôi khi
được vẽ bằng hình ảnh ba
chiều để tạo tính thẩm mỹ, mặc dù việc này
không cung cấp thêm thông tin và không phải là cách biểu diễn được khuyến nghị.
Đối với biểu đồ cột, các
hình chữ nhật không nhất thiết phải liền nhau.
CHÚ THÍCH 2: Sự phân biệt giữa biểu đồ
phân bố và biểu đồ cột ngày
càng trở nên mờ nhạt do phần mềm sẵn có không phải lúc nào cũng tuân thủ các
định nghĩa nêu ở đây.
1.63
Tần số tích
lũy
Tần số (1.59) cộng dồn đối
với các lớp tính đến và bao gồm cả giới hạn quy định.
CHÚ THÍCH: Định nghĩa này chỉ áp dụng cho
các giới hạn quy định tương ứng với các giới hạn lớp (1.56).
1.64
Tần số tương
đối (tần
suất)
Tần số (1.59) chia cho tổng
số lần xuất hiện
hoặc giá trị quan trắc (1.4).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Tần số tương
đối tích lũy (tần suất tích lũy)
Tần số tích lũy (1.63) chia
cho tổng số lần xuất hiện hoặc giá trị quan trắc (1.4).
2 Thuật ngữ dùng
trong xác suất
2.1
Không gian
mẫu
Ω
Tập hợp tất cả các kết quả có thể có.
VÍ DỤ 1: Xét thời gian pin do người tiêu dùng
mua sử dụng được. Nếu pin không có điện khi sử dụng lần đầu thì thời gian sử
dụng bằng 0. Nếu pin hoạt động trong một khoảng thời gian thì thời gian sử dụng bằng một số
giờ. Do đó, không gian mẫu gồm các kết quả {pin hỏng ngay lần đầu} và {pin hỏng
sau x giờ, trong
đó x lớn hơn 0}. Ví
dụ này sẽ được sử dụng trong toàn bộ điều này. Cụ thể, thảo luận mở
rộng của ví dụ này được nêu trong 2.68.
VÍ DỤ 2: Một hộp gồm 10 điện trở được
ghi nhãn 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Nếu hai điện trở được lấy mẫu ngẫu
nhiên không hoàn lại từ bộ điện trở này, thì không gian mẫu gồm 45 kết quả sau:
(1,
2),
(1,
3),
(1, 4), (1, 5), (1,6), (1, 7), (1, 8), (1, 9), (1, 10), (2, 3), (2, 4), (2, 5), (2, 6), (2,
7), (2, 8), (2, 9), (2,
10), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (3, 9), (3, 10), (4, 5), (4, 6), (4, 7),
(4, 8), (4, 9), (4, 10), (5, 6), (5, 7), (5, 8), (5, 9), (5, 10), (6,
7), (6, 8), (6, 9), (6, 10), (7, 8), (7, 9), (7, 10), (8, 9), (8, 10), (9, 10).
Biến cố (1, 2) được coi là giống với (2, 1), vậy thứ tự lấy mẫu điện trở không
quan trọng. Nếu thứ tự là quan trọng thì (1, 2) được coi là khác với (2, 1), khi đó
có tổng số 90 kết quả trong không gian mẫu.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Các kết quả có thể phát
sinh từ thực nghiệm thực tế hoặc thực nghiệm giả thuyết hoàn toàn. Tập hợp này có
thể là danh sách rõ ràng, một tập hợp đếm được ví dụ như các số nguyên dương,
{1, 2, 3, ...}, hoặc đường thẳng thực.
CHÚ THÍCH 2: Không gian mẫu là thành
phần đầu tiên của không gian xác suất (2.68).
2.2
Biến cố
A
Tập con của không gian mẫu (2.1)
VÍ DỤ 1: Tiếp theo ví dụ 1 của 2.1,
dưới đây là các ví dụ
về biến cố {0}, (0, 2), {5,7}, [7, +∞), ứng
với pin hỏng ngay từ đầu, pin ban đầu hoạt động nhưng chưa đến hai giờ làm việc
thì hỏng, pin hỏng ở chính
xác là 5,7 h, và sau 7 h pin vẫn không hỏng. {0} và {5,7} mỗi tập chứa một giá
trị; (0, 2) là khoảng mở của đường thẳng thực; [7, +∞) là khoảng vô hạn
đóng bên trái của đường thẳng thực.
VÍ DỤ 2: Tiếp theo ví dụ 1 của 2.1, lưu ý đến
việc chọn mà không hoàn lại và không ghi lại thứ tự chọn. Một biến cố có thể
xảy ra là 4 định nghĩa bởi {ít nhất một trong các điện trở 1 hoặc 2 nằm trong mẫu}. Biến cố này chứa 17 kết
quả (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9), (1, 10), (2, 3), (2, 4), (2, 5),
(2,
6)
, (2, 7), (2, 8), (2, 9) và (2, 10). Một biến cố khác là B {không có điện trở
nào trong số 8, 9 hoặc 10 nằm trong mẫu}. Biến cố này chứa 21 kết quả
(1,
2),
(1,3), (1, 4), (1, 5), (1, 6), (1, 7), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7),
(3, 4), (3, 5), (3, 6), (3, 7), (4, 5), (4, 6), (4, 7), (5, 6), (5, 7),
(6,7).
VÍ DỤ 3: Tiếp tục với ví dụ 2, phần giao nhau giữa
biến cố A và B (nghĩa là
một trong các điện trở 1 và 2 nằm trong mẫu nhưng không có điện trở nào trong số 8, 9 và
10), chứa 11 kết quả sau: (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(1, 7), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Số kết quả trong hợp của hai biến cố A và B
(nghĩa là ít nhất một trong hai điện trở 1 và 2 hoặc không có điện trở nào
trong số 8, 9 và 10 nằm trong mẫu) là 27 đúng bằng 17 + 21 - 11, là số kết quả
trong A cộng số kết
quả trong B trừ đi số kết quả trong phần giao nhau của hai
biến cố.
CHÚ THÍCH: Cho trước biến cố và kết
quả của thực nghiệm, biến cố được gọi là xảy ra nếu kết quả thuộc về biến cố
đó. Các biến cố thực tế sẽ thuộc về sigma đại số của các biến cố (2.69),
thành phần thứ hai của không gian xác suất (2.68). Các biến cố tự nhiên
xảy ra trong trường hợp trò chơi may rủi (bài poke, rulet, ...) xác định số kết
quả thuộc về biến cố xác định các số chênh để cá cược.
2.3
Biến cố bù
AC
Không gian mẫu (2.1) loại
đi biến cố (2.2) đã cho.
VÍ DỤ 1: Tiếp tục với pin ở ví dụ 1
của 2.1, phần bù của biến cố {0} là biến cố (0, +∞) tương đương với phần bù của
biến cố ban đầu pin hoạt động. Tương tự, biến cố [0,3) ứng với các trường hợp
pin ban đầu không hoạt động hoặc hoạt động trong khoảng ít hơn ba giờ. Phần bù
của biến cố này là [3, ∞) ứng với trường hợp pin làm việc ở 3 h và thời gian
làm việc lớn hơn giá trị này.
VÍ DỤ 2: Tiếp tục với ví dụ 2 của 2.2.
Có thể dễ dàng tìm ra số kết quả trong biến cố B bằng cách
xem xét biến cố bù cho B = {mẫu chứa ít nhất một trong các điện trở 8, 9 hoặc 10}. Biến cố này
chứa 7 + 8 + 9 = 24 kết quả (1, 8), (2, 8), (3, 8), (4, 8), (5, 8), (6, 8), (7, 8) , (1, 9),
(2, 9), (3, 9), (4, 9), (5, 9), (6, 9), (7, 9), (8, 9) , (1, 10),
(2, 10), (3, 10), (4, 10), (5, 10), (6, 10), (7, 10) , (8,
10), (9, 10). Vì toàn bộ
không gian mẫu chứa 45 kết quả nên biến cố B chứa 45 - 24 = 21
kết quả [đó là: (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (2,
3), (2, 4), (2, 5), (2, 6), (2, 7), (3, 4), (3, 5), (3, 6), (3, 7), (4, 5), (4,
6), (4, 7), (5, 6), (5, 7), (6, 7)].
CHÚ THÍCH 1: Biến cố bù là phần bù của
biến cố trong không gian mẫu.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Đối với biến cố A, biến
cố bù cho A thường được kí hiệu là Ac.
CHÚ THÍCH 4: Trong nhiều trường hợp, có thể dễ
dàng tính toán xác suất của phần bù của một biến cố hơn là tính xác
suất của biến cố đó. Ví dụ, biến cố xác định bởi “ít nhất một khuyết tật xuất
hiện trong mẫu gồm 10 cá thể được chọn ngẫu nhiên từ tổng thể gồm 1 000 cá thể,
với giả định một phần trăm khuyết tật” có một lượng lớn các kết quả được liệt
kê. Phần bù của biến cố này (không phát hiện thấy khuyết tật) dễ xử lí hơn nhiều.
2.4
Biến cố độc
lập
Cặp biến cố (2.2) sao cho xác
suất (2.5) của phần giao nhau giữa hai biến cố đó là tích của các
xác suất riêng lẻ.
VÍ DỤ 1: Xét trường hợp trò tung hai
xúc xắc, một đỏ và một trắng có được 36 kết quả, mỗi kết quả có xác suất 1/36. Di được định
nghĩa là biến cố trong đó
tổng số chấm trên hai xúc xắc là i. W được định nghĩa là
xúc xắc trắng có một chấm. Biến cố D7 và W độc lập
nhau, trong khi biến cố Di và W lại không
độc lập với i = 2, 3, 4, 5 hoặc 6. Các biến cố không độc lập được gọi là biến
cố phụ thuộc.
VÍ DỤ 2: Các biến cố độc lập và phụ thuộc xảy
ra tự nhiên trong các ứng dụng. Trong trường hợp các biến cố hoặc tình huống là phụ
thuộc thì việc biết kết quả của biến cố liên quan rất có ích. Ví
dụ, một người chuẩn bị thực hiện một cuộc phẫu thuật tim sẽ có khả năng thành công rất khác
nhau, nếu đó là trường hợp người này có tiền sử hút thuốc hoặc yếu tố rủi ro khác. Vì vậy, hút
thuốc và chết do tiến triển bệnh là phụ thuộc. Ngược lại, cái chết có thể độc
lập với ngày của tuần mà người này sinh ra. Trong ngữ cảnh độ tin cậy
thì các thành phần có nguyên nhân hỏng chung thì không có thời gian
làm việc đến khi hỏng độc lập. Các thanh nhiên liệu trong lò phản ứng có xác
suất thấp xảy ra vỡ nhưng đưa ra rằng một thanh nhiên liệu bị gãy thì xác suất
gãy thanh liền kề về cơ bản có thể tăng lên.
VÍ DỤ 3: Tiếp theo ví dụ 2 của 2.2,
giả định rằng việc lấy mẫu được thực hiện bằng cách lấy mẫu ngẫu nhiên đơn
giản, sao cho tất cả các kết quả có cùng xác suất 1/45. Khi đó P(A) =
17/45 = 0,377 8, P(B) = 21/45 = 0,4667 và P (A và B)
= 11/45 = 0,244 4. Tuy nhiên, tích P(A) x P(B) = (17/45) x (21/45) =
0,176 3, khác với 0,244 4, do đó biến cố A và B là không độc lập.
CHÚ THÍCH: Định nghĩa này được nêu
trong ngữ cảnh hai biến cố nhưng có thể mở rộng thêm. Đối với biến cố A và B, điều kiện
độc lập P(A Ո B) = P(A) P(B). Đối với ba
biến cố A,
B và C độc lập,
điều kiện là:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
P(A Ո B) = P (A) P (B)
P(A Ո C) = P(A)
P(C) và
P (B Ո C) = P (B) P (C)
Nói chung, đối với nhiều hơn hai biến
cố, A1, A2, .... An là độc lập
nếu xác suất phần giao nhau của tập con các biến cố cho trước bất kỳ bằng tích
xác suất các biến cố riêng lẻ, điều kiện này duy trì cho từng và mọi tập con.
Có thể đặt ra ví dụ trong đó mỗi cặp biến cố là độc lập nhưng ba biến cố lại
không độc lập (nghĩa là theo cặp chứ không hoàn toàn độc lập).
2.5
Xác suất của
biến cố A
P(A)
Số thực thuộc khoảng đóng [0, 1] được ấn định
cho một biến cố (2.2).
VÍ DỤ: Tiếp theo ví dụ 2 của 2.1, có
thể tìm được xác suất của một biến cố bằng cách cộng các xác suất của tất cả
các kết quả cấu thành biến cố đó. Nếu tất cả 45 kết quả có cùng một xác suất
thì mỗi kết quả sẽ có xác suất là 1/45.
Xác suất của biến cố có thể tìm được bằng cách đếm số kết quả rồi chia cho 45.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Định nghĩa này đề cập đến
xác suất như là xác suất của một biến cố cụ thể. Xác suất có thể liên quan đến
tần suất xuất hiện trong một thời gian dài hoặc mức độ tin tưởng vào khả
năng xuất hiện biến cố. Thông thường, xác suất của biến cố A được biểu
thị bằng P(A). Ký hiệu 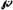 (A) sử dụng chữ
(A) sử dụng chữ 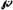 được dùng trong trường hợp có nhu cầu xem
xét rõ ràng sự chính thống
của không gian xác suất (2.68).
được dùng trong trường hợp có nhu cầu xem
xét rõ ràng sự chính thống
của không gian xác suất (2.68).
2.6
Xác suất có
điều kiện
P(A\B)
Xác suất (2.5) của phần giao
nhau giữa biến cố A và B chia cho xác suất của B.
VÍ DỤ 1: Tiếp theo ví dụ 1 của
2.1, xét biến cố (2.2) A xác định là {pin hoạt động
trong ít nhất là ba giờ}, là [3, ∞).
Biến cố B được xác định là {pin hoạt động ngay từ đầu}, là (0, ∞).
Xác suất có điều kiện của A cho trước B tính đến việc xử lý
trường hợp pin hoạt động từ ban đầu.
VÍ DỤ 2: Tiếp theo ví dụ 2 của 2.1,
nếu là lựa chọn không hoàn lại, xác suất chọn điện trở 2 trong lần lấy mẫu thứ
hai là bằng không nếu biết trước nó đã được chọn trong lần lấy mẫu thứ nhất.
Nếu các xác suất đối với mọi điện trở được chọn là bằng nhau thì xác suất chọn
điện trở 2 trong lần lấy mẫu thứ hai bằng 0,111 1 nếu biết trước nó không được
chọn trong lần lấy mẫu thứ nhất.
VÍ DỤ 3: Tiếp tục với ví dụ 2 của 2.1,
nếu là lựa chọn có hoàn lại và
các xác suất bằng nhau đối với tất cả các điện trở được chọn trong mỗi lần lấy
mẫu thì xác suất chọn điện trở 2 trong lần lấy thứ hai sẽ là 0,1 hoặc là điện
trở 2 đã được chọn trong lần đầu hoặc là không được chọn trong lần đầu. Vì vậy
các kết quả của lần lấy mẫu thứ nhất và thứ hai là các biến cố độc lập.
CHÚ THÍCH 1: Xác suất của biến cố B
cần phải lớn hơn không.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Nếu xác suất có điều kiện
của biến cố A cho trước biến cố B xảy ra bằng xác suất xảy ra
biến cố A, thì khi đó biến cố A và B là độc lập. Nói cách
khác, việc biết được sự xuất hiện của B không ảnh hưởng đến xác
suất của A.
2.7
Hàm phân bố
của biến ngẫu nhiên X
F(x)
Hàm số của x cho biết xác
suất (2.5) của biến cố (2.2) (-∞,x].
CHÚ THÍCH 1: Khoảng (-∞, x] là tập hợp
tất cả các giá
trị nhỏ hơn và bao gồm cả x.
CHÚ THÍCH 2: Hàm phân bố mô
tả toàn bộ phân
bố
xác
suất
(2.11) của biến ngẫu nhiên (2.10). Phân loại phân bố cũng như phân loại
biến ngẫu nhiên thành các lớp rời rạc hoặc liên tục đều dựa trên phân loại hàm
phân bố.
CHÚ THÍCH 3: Vì biến ngẫu nhiên lấy
giá trị là các số thực hoặc bộ có thứ tự của k số thực, hàm ý trong định
nghĩa này là x cũng là một
số thực hoặc bộ có thứ tự của k số thực. Hàm phân bố đối với phân bố
nhiều chiều (2.17) cho biết xác suất (2.5) mà mỗi biến ngẫu nhiên đơn
của phân bố nhiều chiều nhỏ hơn hoặc bằng giá trị quy định, về ký
hiệu, hàm phân bố nhiều chiều được cho bởi F(x1, x2, …, xn) = P[X1 ≤
x1, X2 ≤ x2, …, Xn ≤ xn].
Hàm
phân bố cũng là hàm không giảm. Trường hợp một chiều, hàm phân bố được cho bởi F(x) = P[X ≤ x], đưa ra xác
suất của
biến
cố là biến ngẫu nhiên X lấy các giá trị nhỏ hơn hoặc bằng x.
CHÚ THÍCH 4: Thông thường, hàm
phân bố được chia thành: hàm phân bố rời rạc (2.22) và hàm phân bố
liên tục (2.23) nhưng cũng có các khả năng khác. Trở lại ví dụ về pin ở
2.1, hàm phân bố có thể như sau:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Từ quy định về hàm phân bố này, tuổi
thọ của pin là không âm. Có 10 % cơ hội pin không hoạt động ngay từ lần đầu.
Nếu trên thực tế ban đầu pin không hoạt động thì tuổi thọ của pin có phân bố
mũ (2.58) với tuổi thọ trung bình là 1 h.
CHÚ THÍCH 5: Chữ viết tắt cdf (hàm
phân bố tích lũy) thường được dùng cho
hàm phân bố.
2.8
Họ phân bố
Tập hợp các phân bố xác suất
(2.11).
CHÚ THÍCH 1: Tập hợp các phân bố xác suất
thường được xác định bởi tham số (2.9) của phân bố xác suất.
CHÚ THÍCH 2: Trung bình (2.35)
và/hoặc phương sai (2.36) của phân bố xác suất thường được dùng như chỉ
số của họ phân bố hoặc bộ phận của chỉ số trong trường hợp cần nhiều hơn hai
tham số để xác định họ phân bố. Trong các trường hợp khác, trung bình và phương
sai không nhất thiết phải
là các tham số rõ ràng trong họ phân bố mà đúng hơn là hàm của các tham số.
2.9
Tham số
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Tham số có thể là một
chiều hoặc nhiều chiều.
CHÚ THÍCH 2: Tham số đôi khi được gọi
là tham số định vị, đặc biệt nếu tham số tương ứng trực tiếp với trung bình của
họ phân bố. Một số tham số được mô tả như tham số thang đo, đặc biệt nếu
chúng chính là hoặc tỷ lệ với độ lệch chuẩn (2.37) của phân bố. Các tham
số không phải
là
tham số định vị cũng không phải là tham số thang đo thường được gọi là tham số
định dạng.
2.10
Biến ngẫu
nhiên
Hàm xác định trên không gian mẫu
(2.1) trong đó các giá trị của hàm này là bộ có thứ tự của k số thực.
VÍ DỤ: Tiếp theo ví dụ về pin
trong 2.1, không gian mẫu gồm các biến cố được mô tả bằng lời (pin hỏng ngay lần
đầu tiên, ban đầu pin hoạt động nhưng sau đó hỏng ở x giờ). Các
biến cố như vậy khó giải quyết bằng toán học, do đó phải kèm theo mỗi biến cố
thời gian tại đó pin hỏng (cho bằng
số thực). Nếu biến ngẫu nhiên lấy giá trị 0, thì ta có thể thấy rằng kết quả này
tương ứng với sự cố xảy ra ngay từ đầu. Đối với giá trị của biến ngẫu nhiên lớn
hơn không, có thể hiểu là ban đầu pin hoạt động và sau đó hỏng ở giá trị cụ thể
này. Biểu diễn của biến ngẫu nhiên cho phép trả lời câu hỏi: “xác suất pin có
tuổi thọ vượt quá thời gian bảo hành của nó, nghĩa là 6 h, là bao nhiêu?”.
CHÚ THÍCH 1: Ví dụ về bộ k có
thứ tự là (x1, x2, ....xk). Nói cách
khác, bộ có thứ tự k là vectơ k chiều (vectơ hàng hoặc cột).
CHÚ THÍCH 2: Thông thường, biến
ngẫu nhiên có số chiều biểu thị bằng k. Nếu k = 1 thì biến
ngẫu nhiên được gọi là một chiều hoặc một biến. Đối với k > 1, biến
ngẫu nhiên được gọi là nhiều chiều.
Trên thực tế, khi số chiều là một số cho trước, k, biến ngẫu nhiên được
gọi là k chiều.
CHÚ THÍCH 3: Biến ngẫu nhiên một chiều
là hàm giá
trị
thực xác định theo không gian mẫu (2.1) là bộ phận của không gian xác
suất (2.68).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 5: Thành phần thứ j của
biến ngẫu nhiên k-chiều là biến
ngẫu nhiên tương ứng với thành phần thứ j duy nhất của bộ k. Thành
phần thứ j của biến
ngẫu nhiên k chiều tương ứng với không gian xác suất trong đó biến cố
(2.2) chỉ được xác
định về giá trị của thành phần được xét.
2.11
Phân bố xác
suất
Phân bố
Độ đo xác suất (2.70) được
xác định bởi một biến ngẫu nhiên (2.10).
VÍ DỤ: Tiếp theo ví dụ về pin ở 2.1,
phân bố tuổi thọ
của
pin mô tả hoàn toàn các xác suất xuất hiện các giá trị cụ thể. Không biết chắc
thời gian hỏng của pin sẽ là bao nhiêu cũng như không biết (trước thử nghiệm)
việc pin có hoạt động ngay từ ban đầu hay không. Phân bố xác suất mô tả hoàn
toàn tính chất xác suất của một kết quả không chắc chắn. Trong Chú thích 2 của
2.7, đưa ra một khả năng biểu diễn phân bố xác suất, gọi là hàm phân bố.
CHÚ THÍCH 1: Có nhiều cách biểu diễn
toán học tương đương cho phân bố bao gồm hàm phân bố (2.7), hàm mật
độ xác suất (2.27), nếu có, và hàm đặc trưng. Với các mức độ khó khác nhau,
các cách biểu diễn này cho phép xác định xác suất tại đó biến ngẫu nhiên lấy
giá trị trong vùng đã cho.
CHÚ THÍCH 2: Vì biến ngẫu nhiên là hàm
số từ các tập hợp con của không gian mẫu lên đường thẳng thực nên, chẳng hạn,
xác suất của biến ngẫu nhiên nhận giá trị thực bất kỳ là 1. Đối với ví dụ về
pin, P[X ≥ 0] = 1. Trong nhiều
trường hợp, nếu xử lý trực tiếp biến ngẫu nhiên và một trong các cách thể
hiện của nó sẽ dễ dàng hơn nhiều so với việc liên hệ đến độ đo xác suất. Tuy
nhiên, khi chuyển đổi
từ cách thể hiện này sang cách thể hiện khác, độ đo xác suất đảm bảo được tính
nhất quán.
CHÚ THÍCH 3: Biến ngẫu nhiên có một thành
phần được gọi là phân bố xác suất một chiều hoặc đơn biến. Nếu biến ngẫu nhiên
có hai thành phần, thì đó là phân bố xác suất hai chiều hoặc hai biến, còn nếu có nhiều
hơn hai thành phần thì ta nói rằng biến ngẫu nhiên có phân bố xác suất nhiều
chiều hoặc đa biến.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Kỳ vọng
Tích phân của hàm của biến ngẫu
nhiên (2.10) theo độ đo xác suất (2.70) lấy trên toàn bộ không
gian mẫu (2.1).
CHÚ THÍCH 1: Kỳ vọng của hàm
g của biến ngẫu nhiên X được biểu thị bằng E[g(X)] và được
tính bằng:
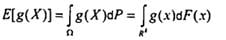
trong đó F(x) là hàm phân
bố tương ứng.
CHÚ THÍCH 2: “E” trong E[g(X)] lấy từ “giá
trị kỳ vọng” hoặc “kỳ
vọng” của biến ngẫu nhiên X. E có thể được coi như một toán tử hoặc hàm
số chiếu biến ngẫu nhiên lên đường thẳng thực theo công thức trên.
CHÚ THÍCH 3: Có hai tích phân được cho
đối với E[g(X)]. Tích phân
đầu tiên lấy trên không gian mẫu chỉ có nghĩa về khái niệm chứ
không dùng trong thực tiễn. Tích phân thứ hai mô tả việc tính toán không gian Rk,
được quan tâm nhiều hơn trong thực tiễn.
CHÚ THÍCH 4: Trong nhiều trường hợp,
tích phân nói trên rút gọn về dạng nhận biết được từ phép tính. Các
ví dụ được cho trong chú thích của moment bậc r (2.34) trong đó g(x)
= xr, trung bình (2.35) trong đó g(x) = x và phương
sai (2.36) trong đó g(x) = [x - E(X)]2.
CHÚ THÍCH 5: Định nghĩa này không giới
hạn ở tích phân một chiều như các ví dụ và chú thích trước. Đối với trường hợp
số chiều lớn hơn, xem 2.43.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.13
p-phân vị
p-fractile
Xp, xp
Giá trị của x bằng cận
dưới của tất cả các x sao cho hàm
phân bố (2.7) F(x) lớn hơn hoặc bằng p, đối với 0 < p
< 1.
VÍ DỤ 1: Xét phân bố nhị thức (2.46) có
hàm khối lượng xác suất cho trong Bảng 2. Tập hợp các giá trị này ứng với phân
bố nhị thức có tham số n = 6 và p = 0,3. Đối với trường
hợp này, một số p-phân vị được
chọn là:
x0,1 = 0
x0,25 = 1
x0,5 = 2
x0,75 = 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
x0,95 = 4
x0,99 = 5
x0,999 = 5
Tính rời rạc của phân bố nhị thức dẫn
đến các giá trị tích phân của các p-phân vị.
Bảng 2 - Ví
dụ về phân bố nhị thức
X
P[X = x]
P[X ≤ x]
P[X > x]
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,117 649
0,117 649
0,882 351
1
0,302 526
0,420 175
0,579 825
2
0,324 135
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,255 690
3
0,185 220
0,929 530
0,070 470
4
0,059 535
0,989 065
0,010 935
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,010 206
0,999 271
0,000 729
6
0,000 729
1,000 000
0,000 000
VÍ DỤ 2: Xét một phân bố chuẩn
chuẩn hóa (2.51) có các giá trị được chọn từ hàm phân bố cho
trong Bảng 3. Một số p-phân vị được chọn là:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
p
x sao cho P[X
≤ x] = p
0,1
-1,282
0,25
-0,674
0,5
0,000
0,75
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,841 344 75
1,000
0,9
1,282
0,95
1,645
0,975
1,960
0,99
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,995
2,576
0,999
3,090
Vi phân bố của X là liên tục
nên tiêu đề của cột thứ hai cũng có thể là: x sao cho P[X<x]=
p.
CHÚ THÍCH 1: Đối với phân bố liên
tục
(2.23), nếu p là 0,5 thì 0,5-phân vị ứng với trung vị (2.14). Đối với p
bằng 0,25, 0,25-phân vị được coi là tứ phân vị dưới. Đối với phân bố liên tục,
25 % của phân bố thấp hơn 0,25 phân vị trong khi 75 % là cao hơn 0,25 phân vị.
Đối với p bằng 0,75, 0,75-phân vị được coi là tứ phân vị trên.
CHÚ THÍCH 2: Nói chung, 100 p % phân bố là
thấp hơn p-phân vị; 100(1 - p) % phân bố cao hơn p-phân
vị. Việc xác định trung vị gặp khó khăn đối với các phân bố rời rạc vì có thể phải
thảo luận vì còn có nhiều
giá trị thỏa mãn
định nghĩa.
CHÚ THÍCH 3: Nếu F liên tục và
tăng ngặt thì p-phân vị là
lời giải cho F(x) = p. Trong
trường hợp này, từ “cận dưới” trong định nghĩa có thể thay bằng “tối thiểu”.
CHÚ THÍCH 4: Nếu hàm phân bố
là hằng số và bằng p trong một khoảng thì tất cả các giá trị
trong khoảng đó là p-phân vị đối với F.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.14
Trung vị
0,5-phân vị (2.13).
VÍ DỤ: Đối với ví dụ về pin ở chú
thích 4 trong 2.7, trung vị là 0,587 8, là lời giải cho x trong 0,1 +
0,9[1-exp(-x)] = 0,5.
CHÚ THÍCH 1: Trung vị là một trong các
p-phân vị
(2.13) được áp dụng phổ
biến nhất trong ứng dụng thực tế. Trung vị của một phân bố một chiều
(2.16) liên tục là giá trị sao cho một nửa của tổng thể (1.1) lớn hơn hoặc bằng
trung vị và một nửa của tổng thể nhỏ hơn hoặc bằng trung vị.
CHÚ THÍCH 2: Trung vị được xác định
cho các phân bố một chiều (2.16)
2.15
Tứ phân vị
0,25-phân vị (2.13) hoặc 0,75-phân
vị.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: 0,25 phân vị cũng được
coi là tứ phân vị dưới, trong khi 0,75 phân vị cũng được gọi là tứ
phân vị trên.
CHÚ THÍCH 2: Tứ phân vị được xác định cho
các phân bố một chiều (2.16).
2.16
Phân bố xác
suất đơn biến
Phân bố một chiều
Phân bố xác suất (2.11) của
một biến ngẫu nhiên (2.10).
CHÚ THÍCH: Phân bố xác suất đơn biến
là một chiều. Phân bố nhị thức (2.46), Poisson (2.47), phân bố
chuẩn (2.50), phân
bố gamma (2.56), phân bố t (2.53), phân bố Weibull (2.63) và phân
bố beta (2.59) là ví dụ của phân bố xác suất một chiều.
2.17
Phân bố xác
suất đa biến
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố xác suất (2.11) của
hai hay nhiều biến ngẫu nhiên (2.10).
CHÚ THÍCH 1: Vì trường hợp phân bố một
chiều phổ biến hơn nên khi không có quy định nào khác thì thường giả định là
phân bố một chiều.
CHÚ THÍCH 2: Phân bố nhiều chiều đôi khi được
gọi là phân bố đồng thời.
CHÚ THÍCH 3: Phân bố đa thức
(2.45), phân bố chuẩn hai chiều (2.65) và phân bố chuẩn đa biến (2.64) là các
ví dụ của phân bố xác suất đa biến được đề cập trong tiêu chuẩn này.
2.18
Phân bố xác
suất biên duyên
Phân bố biên duyên
Phân bố xác suất (2.11) của
một tập hợp con thực sự, không rỗng gồm các thành phần của một biến ngẫu
nhiên (2.10).
VÍ DỤ 1: Đối với một phân bố có ba
biến ngẫu nhiên X, Y và Z, sẽ có ba phân bố biên duyên với hai
biến ngẫu nhiên, đó là (X, Y), (X, Z) và (Y, Z) và ba phân
bố biên duyên có một biến ngẫu nhiên là X, Y và Z.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 3: Đối với phân bố đa thức
(2.45), phân bố của (X1, X2) là phân bố
biên duyên k > 3. Phân bố của X1, X2, …, Xk, riêng rẽ cũng là
các phân bố biên
duyên.
Các phân bố biên duyên này đều là phân bố nhị thức (2.46).
CHÚ THÍCH 1: Đối với phân bố đồng thời
k chiều, một ví dụ về phân bố biên duyên bao gồm phân bố xác suất của
một tập con gồm k1 < k biến
ngẫu nhiên.
CHÚ THÍCH 2: Cho một phân bố xác
suất nhiều chiều (2.17) liên tục (2.23) biểu diễn bởi hàm mật độ
xác suất (2.26), hàm mật độ xác suất của phân bố xác suất biên duyên được xác định
bằng tích phân hàm mật độ xác suất trong phạm vi các biến không được xét trong phân
bố biên duyên.
CHÚ THÍCH 3: Cho một phân bố xác suất
nhiều chiều rời rạc (2.22) biểu diễn bởi hàm khối lượng xác suất
(2.24), hàm khối lượng xác suất của phân bố xác suất biên duyên được xác định
bằng tổng hàm khối lượng xác suất trong phạm vi các biến không được xét trong
phân bố biên duyên.
2.19
Phân bố xác
suất có điều kiện
Phân bố có điều kiện
Phân bố xác suất (2.11) giới
hạn trong tập con không rỗng của không gian mẫu (2.1) và điều chỉnh để
có xác suất của toàn bộ không gian mẫu giới hạn.
VÍ DỤ 1: Trong ví dụ pin ở 2.7, chú
thích 4, phân bố có điều kiện của tuổi thọ pin dựa vào hàm pin ban đầu là hàm
mũ (2.58).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 3: Xét biến ngẫu nhiên X mô tả phân bố
của phí tổn bảo hiểm
hàng năm ở Florida do các biến cố bão được công bố. Phân bố này có xác suất khác không là phí
tổn hàng năm bằng không do khả năng không có bão tác động đến Florida trong một
năm cho trước. Phân bố có điều kiện của phí tổn trong những năm thực tế xảy ra
sự việc có thể là mối quan tâm.
CHÚ THÍCH 1: Như một ví dụ về phân
bố có hai biến ngẫu nhiên X và Y, có các phân bố có điều kiện đối
với X
và
phân bố có điều kiện đối với Y. Phân bố của X lấy điều kiện thông
qua Y =
y được biểu
thị là “phân bố có điều kiện của X cho trước Y = y, trong khi phân
bố của Y lấy điều kiện X = x được biểu thị “phân bố có điều kiện
của Y cho trước X = x”.
CHÚ THÍCH 2: Phân bố xác suất biên
duyên (2.18) có thể coi như phân bố không điều kiện.
CHÚ THÍCH 3: Ví dụ 1 ở trên minh họa
trường hợp phân bố một chiều
được điều chỉnh thông qua điều kiện để có được phân bố một chiều khác, mà trong
trường hợp này là phân bố khác. Ngược lại, đối với phân bố hàm mũ, phân bố có
điều kiện mà sự cố sẽ xảy ra trong giờ tiếp theo, biết rằng không có sự cố nào xảy
ra trong vòng 10 h đầu tiên, là hàm mũ có cùng tham số.
CHÚ THÍCH 4: Phân bố có điều kiện có
thể phát sinh đối với các phân bố rời rạc nhất định trong đó không thể có các kết
quả cụ thể. Ví dụ, phân
bố Poisson có thể dùng như một mô hình đối với số bệnh nhân ung thư trong một
tổng thể gồm các bệnh nhân nhiễm bệnh nếu lấy điều kiện là dương tính hoàn toàn (bệnh nhân
u bướu không được định nghĩa là nhiễm bệnh).
CHÚ THÍCH 5: Phân bố có điều kiện phát
sinh trong ngữ cảnh giới hạn
không gian mẫu về một tập con cụ thể. Đối với (X, Y) có phân
bố chuẩn hai chiều (2.65), có thể quan tâm xét phân bố có điều kiện của (X,
Y) cho trước kết quả phải xuất hiện trong hình vuông đơn vị [0, 1] x [0, 1]. Một
khả năng khác là
phân
bố có điều kiện của (X, Y) cho trước X2 + Y2 ≤ r.
Trường hợp này tương ứng với trường
hợp trong đó ví dụ một bộ phận đáp ứng dung sai và ta có thể quan đến thêm các
tính chất dựa vào
việc đạt được tính năng này.
2.20
Đường hồi quy
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Ở đây, đường
hồi quy được xác định trong ngữ cảnh (X, Y) có phân bố
hai chiều (xem chú thích 1 của 2.17). Do đó, đây là một khái niệm khác với phân tích hồi
quy, trong đó Y liên quan đến tập hợp các giá trị độc lập xác định
trước.
2.21
Mặt hồi quy
Tập hợp các giá trị của kỳ vọng
(2.12) của phân bố xác suất có điều kiện (2.19) của một biến ngẫu
nhiên (2.10) Y cho trước các biến ngẫu nhiên X1 = x1 và X2 = x2.
CHÚ THÍCH: Ở đây, như
trong 2.20, mặt hồi quy được xác định trong ngữ cảnh (Y, X1, X2) là một phân
bố nhiều chiều (2.17). Như với đường hồi quy, mặt hồi quy liên quan đến
khái niệm khác với trong phân tích hồi quy và phương pháp luận về mặt đáp ứng.
2.22
Phân bố xác
suất rời rạc
Phân bố rời rạc
Phân bố xác suất (2.11) trong
đó không gian mẫu Ω (2.1) là hữu hạn hoặc
vô hạn đếm được.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: “Rời rạc” có nghĩa là
không gian mẫu có thể
được cho trong một danh mục hữu hạn hoặc bắt đầu của danh mục vô hạn trong đó
có thứ tự rõ ràng, ví dụ như số khuyết tật là 0, 1, 2, ... Ngoài ra, phân bố
nhị thức tương ứng với không gian mẫu hữu hạn {0, 1, 2, …, n} trong khi
phân bố Poisson tương ứng với không gian mẫu vô hạn đếm được {0, 1, 2,…}
CHÚ THÍCH 2: Các trường hợp có dữ liệu
định tính trong lấy mẫu chấp nhận thuộc về phân bố rời rạc.
CHÚ THÍCH 3: Hàm phân bố (2.7)
của phân bố rời rạc có giá trị rời rạc.
2.23
Phân bố xác
suất liên tục
Phân bố liên tục
Phân bố xác suất (2.11) trong
đó hàm
phân bố (2.7) đánh giá tại x có thể biểu
thị như tích phân của hàm không âm từ -∞ đến x.
VÍ DỤ: Trường hợp có phân bố liên tục
xuất hiện trong hầu hết các trường hợp liên quan đến các biến kiểu dữ
liệu trong các ứng dụng công nghiệp.
CHÚ THÍCH 1: Ví dụ về phân bố liên tục
là phân
bố chuẩn (2.50), phân bố chuẩn chuẩn hóa
(2.51), t (2.53), F (2.55), gamma (2.56), khi bình
phương
(2.57),
hàm mũ (2.58), beta (2.59), đều (2.60), cực trị loại I
(2.61), cực trị loại II (2.62), cực trị loại III (2.63) và loga
chuẩn (2.52).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3. Trường hợp dữ liệu định
lượng trong các ứng dụng lấy mẫu chấp nhận tương ứng với phân bố xác suất liên
tục.
2.24
Hàm khối
lượng xác suất
hàm <phân bố rời rạc> cho biết xác
suất (2.5) để
biến
ngẫu nhiên
(2.10) bằng một giá trị cho trước.
VÍ DỤ 1: Hàm khối lượng xác suất
mô tả biến ngẫu
nhiên X bằng số lượng
mặt ngửa xuất hiện
khi tung ba đồng xu là:
P (X=0) = 1/ 8
P (X = 1) = 3 / 8
P (X = 2) = 3/8
P (X = 3) = 1/8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Hàm khối lượng xác suất có
thể được cho là P(X
= xi) = pi, trong đó X là biến ngẫu nhiên, xi là giá trị
cho trước và pi là xác suất
tương ứng.
CHÚ THÍCH 2: Hàm khối lượng xác suất
được đưa vào trong p-phân vị ví dụ 1 của 2.13 bằng cách sử dụng phân
bố nhị thức (2.46).
2.25
Mốt của hàm
khối lượng xác suất
(Các) giá trị ở đó hàm khối lượng
xác suất (2.24) đạt cực đại địa phương.
VÍ DỤ: Phân bố nhị thức (2.46)
với n = 6 và p = 1/3 là phân bố một mốt có mốt tại 3.
CHÚ THÍCH: Phân bố rời rạc (2.22) là
một mốt nếu hàm khối lượng xác suất của nó chỉ có một mốt, hai mốt
nếu hàm khối lượng xác suất có hai mốt và nhiều mốt nếu hàm khối lượng xác suất
có nhiều hơn hai mốt
2.26
Hàm mật độ
xác suất
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hàm không âm khi lấy tích phân từ -∞
đến x cho giá trị của
hàm phân bố (2.7) tại x của phân bố liên tục (2.23).
VÍ DỤ 1: Nhiều hàm mật độ xác suất được cho
trong việc xác định
phân
bố xác suất thường gặp trong thực tế. Các ví dụ bao gồm phân bố chuẩn
(2.50), chuẩn chuẩn hóa (2.51), t (2.53), F (2.55), gamma
(2.56), khi bình phương (2.57), phân bố mũ (2.58), beta
(2.59), phân bố đều (2.60), phân bố chuẩn nhiều chiều (2.64) và phân
bố chuẩn hai chiều (2.65).
VÍ DỤ 2: Đối với hàm phân bố xác định bởi
F(x) = 3x2 - 2x3 trong đó 0 ≤ x ≤ 1, hàm mật
độ xác suất tương
ứng
sẽ là f(x) = 6x(1
- x) trong đó 0 ≤ x ≤ 1.
VÍ DỤ 3: Tiếp theo ví dụ về pin ở 2.1, không
có hàm mật độ xác suất đi kèm với hàm phân bố quy định, do xác suất dương của
kết quả không. Tuy nhiên, phân bố có điều kiện cho rằng pin hoạt động lúc đầu
có
f(x) = exp(-x)
đối với x > 0 là
hàm mật độ xác suất, tương ứng với phân bố mũ.
CHÚ THÍCH 1: Nếu hàm phân bố F
là khả vi liên tục thì hàm mật độ xác suất là
f(x) = dF(x)/dx
tại điểm x nơi có đạo
hàm.
CHÚ THÍCH 2: Đồ thị của f(x)
theo x đưa ra các
mô tả như đối xứng, đỉnh, đuôi nặng, một mốt, hai mốt, v.v... Đồ thị thích
hợp của f(x) nằm trên
biểu đồ phân bố cung cấp đánh giá bằng mắt về sự phù hợp giữa phân bố thích hợp
và dữ liệu.
CHÚ THÍCH 3: Chữ viết tắt thông dụng
của hàm mật độ xác suất là pdf.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Mode của hàm
mật độ xác suất
(Các) giá trị tại đó hàm mật độ xác
suất (2.26) đạt cực đại địa phương.
CHÚ THÍCH: Phân bố liên tục
(2.23) là một mode nếu hàm mật độ xác
suất của nó chỉ có một mode, hai mode nếu hàm mật độ xác suất có hai mode và
nhiều mode nếu hàm mật độ xác suất có nhiều hơn hai mode.
CHÚ THÍCH 2: Phân bố tại đó các mode tạo
thành một tập hợp liên tục cũng được gọi là một mode.
2.28
Biến ngẫu
nhiên rời rạc
Biến ngẫu nhiên (2.10) có phân
bố rời rạc (2.22).
CHÚ THÍCH: Biến ngẫu nhiên rời rạc được
xem xét trong tiêu chuẩn này bao gồm biến ngẫu nhiên phân bố nhị thức (2.46), Poisson
(2.47), siêu hình học (2.48) và đa
thức (2.45).
2.29
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Biến ngẫu nhiên (2.10) có phân
bố liên tục (2.23).
CHÚ THÍCH: Biến ngẫu nhiên liên tục
được đề cập trong tiêu chuẩn này bao gồm biến ngẫu nhiên phân bố chuẩn (2.50), phân
bố chuẩn chuẩn hóa (2.51), phân bố t (2.53), phân bố F
(2.55), gamma (2.56), khi bình phương (2.57), mũ (2.58), beta
(2.59), phân bố đều (2.60), cực trị loại I (2.61), cực trị
loại II (2.62), cực trị loại III (2.63), loga chuẩn (2.52), chuẩn nhiều
chiều
(2.64) và chuẩn hai chiều I (2.65).
2.30
Phân bố xác
suất quy tâm
Phân bố xác suất (2.11) của biến
ngẫu nhiên quy tâm (2.31).
2.31
Biến ngẫu
nhiên quy tâm
Biến ngẫu nhiên (2.10) có
được bằng cách lấy một biến ngẫu nhiên trừ đi giá trị trung bình (2.35) của
nó.
CHÚ THÍCH 1: Biến ngẫu nhiên quy tâm
có trung bình bằng không.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Nếu biến ngẫu nhiên
X có trung bình (2.35) bằng μ thì biến
ngẫu nhiên tương ứng sẽ là X - μ, có trung
bình bằng không.
2.32
Phân bố xác
suất chuẩn hóa
Phân bố xác suất (2.11) của biến
ngẫu nhiên chuẩn hóa (2.33).
2.33
Biến ngẫu
nhiên chuẩn hóa
Biến ngẫu nhiên quy tâm (2.31) có độ
lệch chuẩn (2.37) bằng 1.
CHÚ THÍCH 1: Biến ngẫu nhiên
(2.10) được tự
động
chuẩn hóa nếu trung bình của nó bằng không và độ lệch chuẩn bằng 1. Phân bố đều
(2.60) trong khoảng (-30.5, 30.5) có trung
bình là không và độ lệch chuẩn bằng 1. Phân bố chuẩn chuẩn hóa (2.51)
đương nhiên là được chuẩn hóa.
CHÚ THÍCH 2: Nếu phân bố (2.11)
của biến ngẫu nhiên X có trung bình (2.35) μ và độ lệch
chuẩn σ, thì biến ngẫu
nhiên chuẩn hóa tương ứng sẽ là (X - μ)/σ.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Momen bậc r
Momen thứ r
Kỳ vọng (2.12) của lũy thừa r
của một biến ngẫu nhiên (2.10).
VÍ DỤ: Xét một biến ngẫu nhiên có hàm mật độ
xác suất (2.26) f(x) = exp(-x) đối với x > 0. Sử
dụng công thức tích phân từng phần, có thể chứng tỏ rằng E(X) = 1, E(X2) = 2, E(X3) = 6 và E(X4) = 24, hoặc
nói chung, E(Xr) = r. Đây là ví dụ
của phân bố mũ (2.58).
CHÚ THÍCH 1: Trong trường hợp rời rạc
một chiều, công thức tương ứng:
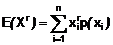
đối với số hữu hạn n kết quả và

đối với số kết quả vô hạn đếm
được. Trong trường hợp liên tục một chiều, công thức tương ứng:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Nếu biến ngẫu nhiên có k
chiều thì lũy thừa r được hiểu là áp dụng cho thành phần.
CHÚ THÍCH 3: Momen được nêu ở đây sử
dụng biến ngẫu nhiên X nâng lên một lũy thừa. Một cách tổng quát hơn, ta có
thể xét momen bậc r của X - μ hoặc (X - μ)/σ.
2.35 Trung
bình
2.35.1
Trung bình
Mômen bậc r = 1
μ
Mômen <phân bố liên tục> bậc r
trong đó r bằng 1, tính như tích phân của tích giữa x và hàm mật
độ xác suất (2.26), f(x), lấy trên đường thẳng thực.
VÍ DỤ 1: Xét biến ngẫu nhiên liên tục
(2.29) X có hàm mật độ xác suất f(x) = 6x(1
-
x), trong đó 0 ≤ x ≤
1.
Trung bình của X
là.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 2: Tiếp theo ví dụ pin từ 2.1 và 2.7, trung
bình là 0,9 vì với xác
suất 0,1 trung bình của phần rời rạc của phân bố là 0 và với xác suất 0,9 trung
bình của phần liên tục của phân bố là 1. Phân bố này là phân bố hỗn hợp liên
tục và rời rạc.
CHÚ THÍCH 1: Trung bình
của phân bố liên tục (2.23) được biểu thị bằng E(X) và được tính
là:
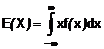
CHÚ THÍCH 2: Trung bình không tồn tại
đối với tất cả các biến ngẫu nhiên (2.10). Ví dụ, nếu X được xác
định bằng hàm mật độ xác suất f(x) = [π(1 + x2)]-1,
tích phân tương ứng với E(X) là phân kỳ.
2.35.2
Trung bình
μ
tổng <phân bố rời rạc> tích của xi và hàm
khối lượng xác suất (2.24) p(xi).
VÍ DỤ 1. Xét biến ngẫu nhiên rời rạc X
(2.28) đại diện cho số mặt ngửa xuất hiện khi tung ba đồng xu. Hàm khối lượng xác
suất là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
P(X = 1) = 3/8
P(X=2) = 3/8
P(X = 3) = 1/8
Vì vậy, trung bình của X là
0(1/8) + 1(3/8) + 2(3/8) + 3(1/8) =
12/8 = 1,5
VÍ DỤ 2: Xem ví dụ 2 trong 2.35.1.
CHÚ THÍCH: Trung bình của phân bố
rời rạc (2.22) biểu thị bằng E(X) và được tính là:
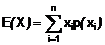
đối với số lượng hữu hạn các kết quả,
và
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
đối với số lượng kết quả vô hạn đếm
được.
2.36
Phương sai
V
Môment bậc r (2.34)
trong đó r bằng 2 theo phân bố xác suất quy tâm (2.30) của biến ngẫu
nhiên (2.10).
VÍ DỤ 1: Đối với biến ngẫu nhiên
rời rạc (2.28) trong ví dụ của 2.24 phương sai là
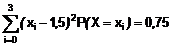
VÍ DỤ 2: Đối với biến ngẫu nhiên
liên tục (2.29) trong ví dụ 1 của 2.26, phương sai là
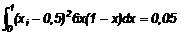
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH: Phương sai có thể xác định
tương đương như kỳ vọng (2.12) của bình phương biến ngẫu nhiên trừ đi trung
bình (2.35) của nó. Phương sai của biến ngẫu nhiên X được ký hiệu
bằng V(X) = E{[X-E(X)]2}.
2.37
Độ lệch chuẩn
σ
Căn bậc hai dương của phương sai
(2.36)
VÍ DỤ: Đối với ví dụ về pin của 2.1 và
2.7, độ lệch chuẩn là 0,995.
2.38
Hệ số biến động
CV
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ: Đối với ví dụ về pin của 2.1 và
2.7, hệ số biến động là 0,99/0,995 bằng 0,994 97.
CHÚ THÍCH 1: Hệ số biến động thường
được tính bằng phần trăm.
CHÚ THÍCH 2: Thuật ngữ “độ lệch chuẩn
tương đối” trước đây không giống với thuật ngữ hệ số biến động.
2.39
Hệ số bất đối
xứng
γ1
Mômen bậc 3 (2.34)
trong phân bố xác suất chuẩn hóa (2.32) của một biến ngẫu nhiên
(2.10).
VÍ DỤ: Tiếp theo ví dụ pin của 2.1 và
2.7 có phân bố hỗn hợp liên tục-rời rạc, sử dụng các kết quả từ ví dụ ở 2.34,
ta có
E(X) = 0,1(0) + 0,9(1) =
0,9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
E(X3)= 0,1(0) +
0,9(6) = 5,4
E(X4) = 0,1(0) +
0,9(24) = 21,6
Để tính hệ số bất đối xứng, lưu ý là E
{[X- E(X)]3}
= E(X3) - 3 E(X) E(X2) + 2 [E(X)]3
và từ 2.37 có độ lệch chuẩn là 0,995. Do đó, hệ số bất đối xứng là [5,4 -
3(0,9)(1,8) + 2(0,9)3]/(0,995)3 hoặc 1,998.
CHÚ THÍCH 1: Một định nghĩa tương
đương dựa trên kỳ vọng (2.12) bậc ba của (X-μ)/σ, là E[((X-μ)3/σ3].
CHÚ THÍCH 2: Hệ số bất đối xứng là thước đo
tính đối xứng của phân bố (2.11) và đôi khi được ký hiệu bằng √β1. Đối với các
phân bố đối xứng, hệ số bất đối xứng bằng 0 (với điều kiện tồn tại mômen
thích hợp trong định nghĩa). Ví dụ về phân bố có độ bất đối xứng bằng không bao
gồm phân bố chuẩn (2.50), phân bố beta (2.59) với điều kiện α
= β và phân bố t (2.53) với điều kiện có các mômen.
2.40
Hệ số nhọn
β2
Mômen bậc 4 (2.34)
trong phân bố xác suất chuẩn hóa (2.32) của một biến ngẫu nhiên (2.10).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
E{[X-E(X)]4} = E(X4) - 4 E(X) E(X3)
+
6[E(X)]2 E(X2)- 3 [E(X)]4
Do đó, hệ số nhọn bằng
[21,6 - 4(0,9)(5,4) + 6(0,9)2(2)
- 3(0,9)4]
/ (0,995)4 hoặc 8,94.
CHÚ THÍCH 1: Một định nghĩa tương
đương dựa trên
kỳ
vọng
(2.12) bậc bốn của (X - μ)/σ, gọi là E[{X-μ)4/σ4].
CHÚ THÍCH 2: Hệ số nhọn là thước đo độ
lớn phần đuôi của phân bố (2.11). Đối với phân bố đều (2.60), hệ
số nhọn là 1,8; đối với phân bố chuẩn (2.50), hệ số nhọn là 3; đối với phân
bố mũ (2.58), hệ số nhọn là 9.
CHÚ THÍCH 3: Cần chú ý khi
xem xét các giá trị nhọn được công bố, vì một số người thực hiện trừ đi 3 (hệ
số nhọn của phân bố chuẩn)
từ giá trị được tính theo định
nghĩa.
2.41
Mômen hỗn hợp
bậc r và s
Trung bình (2.35) của tích lũy thừa
bậc r của một biến ngẫu nhiên (2.10) và bậc s của một biến
ngẫu nhiên khác lấy theo phân bố xác suất (2.11) đồng thời của
chúng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Mômen hỗn hợp
quy tâm bậc r và s
Trung bình (2.35) tích lũy thừa
bậc r của biến ngẫu nhiên quy tâm (2.31) và bậc s của một
biến ngẫu nhiên
quy tâm khác trong phân bố xác suất (2.11) đồng thời của chúng.
2.43
Hiệp phương
sai
σXY
Trung bình (2.35) của tích hai biến
ngẫu nhiên quy tâm (2.31) lấy theo phân bố xác suất (2.11) đồng thời
của chúng.
CHÚ THÍCH 1: Hiệp phương sai là mômen
trung tâm hỗn hợp bậc 1 và 1 (2.42) đối với hai biến ngẫu nhiên.
CHÚ THÍCH 2: Về ký hiệu, hiệp
phương sai là
E[(X-μX)(Y-μY)].
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.44
Hệ số tương
quan
Trung bình (2.35) của tích hai
biến ngẫu nhiên chuẩn hóa (2.33) lấy
theo phân bố xác suất (2.11) đồng thời của chúng.
CHÚ THÍCH: Hệ số tương quan đôi khi
được gọi tắt đơn giản là tương quan. Tuy nhiên, việc sử dụng này lại chồng chéo
với cách giải thích về tương quan như sự liên kết giữa hai biến.
2.45
Phân bố đa
thức
Phân bố rời rạc (2.22) có hàm
khối lượng xác
suất
(2.24)
P(X1 = x1, X2
= x2,… Xk = xk)
= 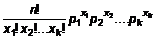
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
x1, x2, ..., xk
là
các số nguyên dương sao cho x1 + x2 + … + xk
= n
với các tham số pi > 0 đối với tất cả i = 1, 2, …, k với p1
+ p2 + … + pk = 1
k số nguyên
lớn hơn hoặc
bằng
2
CHÚ THÍCH: Phân bố đa thức cho biết
xác suất để trong n phép thử độc lập có được một tổ hợp cho trước về số
lần xuất hiện các biến cố trong đó k kiểu biến cố loại trừ nhau, giả
định rằng xác suất xuất hiện của mỗi loại biến cố là như nhau trong tất cả các
phép thử.
2.46
Phân bố nhị
thức
Phân bố rời rạc (2.22) có hàm
khối lượng xác suất (2.24)

trong đó x = 0, 1, 2, …, n và với các tham số n = 1, 2, …, và 0
< p < 1.
VÍ DỤ: Hàm khối lượng xác suất mô tả
trong ví dụ 1 của 2.24 có thể thấy là tương ứng với phân bố nhị thức với các
tham số xác định n = 3 và p = 0,5.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Phân bố nhị thức cho xác
suất về số lần một trong số hai kết quả xảy ra trong n phép thử độc
lập, trong đó mỗi phép thử có cùng hai biến
cố (2.2) loại trừ nhau và xác suất (2.5) của mỗi biến cố là như nhau
đối với các phép thử.
CHÚ THÍCH 3: Trung bình (2.35) của
phân bố nhị thức bằng np. Phương sai (2.36) của phân bố nhị thức
bằng np(1 -p).
CHÚ THÍCH 4: Hàm khối lượng xác suất
nhị thức cũng có thể biểu thị bằng cách sử dụng hệ số nhị thức cho bởi
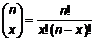
2.47
Phân bố
Poisson
Phân bố rời rạc (2.22) có hàm
khối lượng xác suất (2.24)
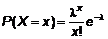
trong đó x = 0, 1,
2,... và tham số λ > 0.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Trung bình (2.35)
và phương sai (2.36) của phân bố Poisson đều bằng λ.
CHÚ THÍCH 3: Hàm khối lượng xác
suất (2.24) của phân bố Poisson cho xác suất về số lần xuất hiện một tính chất của một quá
trình trong một khoảng thời gian bằng độ dài đơn vị đáp ứng các điều kiện nhất
định, ví dụ cường độ xuất hiện phụ thuộc vào thời gian.
2.48
Phân bố siêu
hình học
Phân bố rời rạc (2.22) có hàm
khối lượng xác
suất
(2.24)
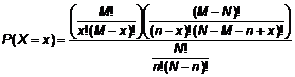
trong đó max (0, M - N) ≤ x ≤ min (M,
n) có tham số là số nguyên
N = 1, 2, ...
M = 0, 1, 2, …, N-1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Phân bố (2.11)
siêu hình học xuất hiện khi số cá thể được đánh dấu trong một mẫu ngẫu nhiên
đơn giản (1.7) cỡ n, được lấy mà không hoàn
lại, từ một tổng thể (hoặc lô) cỡ N chứa chính xác M cá thể
đánh dấu.
CHÚ THÍCH 2: Việc hiểu về phân bố siêu
hình học sẽ dễ dàng hơn khi tham khảo Bảng 4.
Bảng 4 - Ví
dụ về phân bố siêu hình học
Tập hợp
tham chiếu
Cá thể đánh dấu
hoặc không đánh dấu
Cá thể đánh
dấu
Cá thể
không đánh dấu
Tổng thể
N
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
N - M
Các cá thể trong mẫu
n
x
N - x
Các cá thể ngoài
mẫu
N - n M - x
N - n - M + x
CHÚ THÍCH 3: Trong những điều kiện nhất định (ví dụ
n tương đối nhỏ so với N), thì phân bố siêu hình học có thể
xấp xỉ bằng
phân bố nhị thức n và p = M/N.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
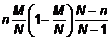
2.49
Phân bố nhị
thức âm
Phân bố rời rạc (2.22) có hàm
khối lượng xác suất (2.24)
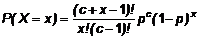
trong đó x = 0, 1, 2, …, n, với tham số c > 0 và tham số p thỏa
mãn 0 < p < 1.
CHÚ THÍCH 1: Nếu c = 1, phân bố
nhị thức âm được coi là phân bố hình học và mô tả xác suất (2.5) biến
cố (2.2) có xác suất là p, sẽ xuất hiện lần đầu tiên trong phép thử
thứ (x + 1).
CHÚ THÍCH 2: Hàm khối lượng xác suất
cũng có thể viết theo cách tương đương như sau:
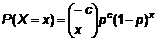
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Dạng hàm khối lượng xác
suất nêu trong định nghĩa này thường được gọi là “phân bố Pascal” với điều kiện
c là số nguyên lớn hơn hoặc bằng 1. Trong trường hợp đó, hàm khối
lượng xác suất mô tả xác suất lần xuất hiện thứ c của biến cố
(2.2), có xác suất (2.5) là p, xuất hiện trong lần thử (c
+ x).
CHÚ THÍCH 4: Trung bình (2.35)
của phân bố nhị thức âm
là (cp)l(1 - p).
Phương sai (2.36) của
nhị
thức
âm là (cp)/(1 - p)2.
2.50
Phân bố chuẩn
Phân bố Gaussian
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
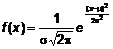
trong đó -∞ < x < ∞ và có
tham số -∞ < μ < ∞ và σ > 0.
CHÚ THÍCH 1: Phân bố chuẩn là một
trong các phân bố xác suất (2.11) được sử dụng rộng rãi nhất trong thống
kê ứng dụng. Do dạng của hàm mật độ, nó thường được gọi là đường “hình chuông”.
Bên cạnh việc sử dụng như một mô hình dùng cho các hiện tượng ngẫu nhiên, phân
bố này còn như phân bố trung bình (1.15) giới hạn. Như một phân bố tham chiếu
trong thống kê, phân bố này được sử dụng rộng rãi để đánh giá tính bất thường của
các kết quả thực nghiệm.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.51
Phân bố chuẩn
chuẩn hóa
Phân bố Gaussian chuẩn hóa
Phân bố chuẩn (2.50) có μ =
0 và σ
=
1.
CHÚ THÍCH: Hàm mật độ xác suất (2.26) của
phân bố chuẩn chuẩn hóa là
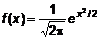
trong đó -∞ < x < ∞. Các bảng
phân bố chuẩn có hàm mật độ xác suất này, đưa ra làm ví dụ, vùng phủ f
đối với các giá trị trong khoảng (-∞, ∞).
2.52
Phân bố lôga
chuẩn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
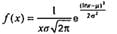
trong đó x > 0 và với các tham số -∞ < μ < ∞ và σ > 0.
CHÚ THÍCH 1: Nếu Y có phân
bố chuẩn (2.50) với trung bình (2.35) μ và độ lệch
chuẩn (2.37) σ, thì phép biến đổi cho bởi X = exp(Y) có hàm mật
độ xác suất nêu trong định nghĩa. Nếu X có phân bố lôga chuẩn có hàm mật
độ xác suất như nêu trong định nghĩa thì ln(X) có phân bố chuẩn
với trung bình μ và độ lệch chuẩn σ.
CHÚ THÍCH 2: Trung bình của phân bố
lôga chuẩn là exp[μ + (σ2)/2] và phương sai là exp(2μ + σ2)
x [exp(σ2) - 1]. Điều
này chỉ ra rằng trung bình và phương sai của phân bố lôga chuẩn là hàm số của
tham số μ và σ2.
CHÚ THÍCH 3: Phân bố lôga chuẩn và phân
bố Weibull (2.63) được sử
dụng phổ biến trong các ứng dụng liên quan tới độ tin cậy.
2.53
Phân bố t
Phân bố Student
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
trong đó -∞ < t < ∞ và với tham
số v, là số
nguyên dương.
CHÚ THÍCH 1: Phân bố t được sử
dụng rộng rãi trong thực tế để đánh giá trung bình mẫu (1.15) trong
trường hợp chung khi độ lệch chuẩn của tổng thể được ước lượng từ dữ liệu.
Thống kê mẫu t có thể so sánh với phân bố t có n - 1 bậc tự
do để đánh
giá
trung
bình quy định như mô tả của trung bình tổng thể thực.
CHÚ THÍCH 2: Phân bố t phát sinh
như phân bố thương số của hai biến ngẫu nhiên (2.10) độc lập, trong đó
tử số có phân bố chuẩn chuẩn hóa (2.51) và mẫu số được phân bố theo căn
bậc hai dương của phân bố khi bình phương (2.57) sau khi chia cho số bậc
tự do của nó. Tham số v được gọi là bậc
tự do (2.54).
CHÚ THÍCH 3: Hàm gamma được định nghĩa
trong 2.56.
2.54
Bậc tự do
v
Số các số hạng trong một tổng trừ đi
số các ràng buộc đối với các số hạng của tổng đó.
CHÚ THÍCH: Khái niệm này đã gặp trước
đây trong ngữ cảnh sử dụng n 1
trong
mẫu số của hàm ước lượng (1.12) của phương sai mẫu (1.16). Số bậc tự do
được dùng để hiệu chỉnh các tham số. Thuật ngữ bậc tự do cũng được sử dụng rộng
rãi trong ISO 3534-3
trong đó bình phương trung bình được cho như tổng các bình phương chia cho số
bậc tự do thích hợp.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố F
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
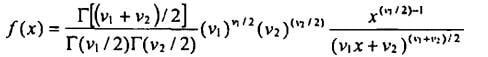
trong đó
x > 0
v1 và v2
là số nguyên
dương
Γ là hàm gamma xác định trong 2.56.
CHÚ THÍCH 1: Phân bố F là phân bố
tham chiếu hữu ích để đánh giá tỉ số của các phương sai (2.36) độc lập.
CHÚ THÍCH 2: Hàm F phát sinh
khi phân bố là
thương
số của hai biến ngẫu nhiên độc lập, mỗi biến có một phân bố khi bình phương
(2.57), chia cho bậc tự do (2.54) của nó. Tham số v1 bậc tự do ở
tử số còn v2 là bậc tự do mẫu số của phân bố F.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố gamma
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
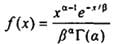
trong đó x > 0 và các
tham số α
>
0, β
>
0.
CHÚ THÍCH 1: Phân bố gamma được sử
dụng trong các ứng dụng liên quan tới độ tin cậy đối với mô hình thời gian tính đến khi
hỏng. Phân bố này bao gồm phân
bố mũ (2.58) như trường hợp đặc biệt cũng như các trường hợp khác với tỷ lệ
hỏng tăng theo tuổi đời.
CHÚ THÍCH 2: Phân bố gamma được xác định
bởi
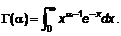
Đối với các giá trị nguyên của α,
Γ(α) =(α - 1)!
CHÚ THÍCH 3: Trung bình (2.35)
của phân bố gamma là αβ. Phương sai (2.36) của phân bố gamma là αβ2.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố
khi-bình phương
Phân bố x2
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26).
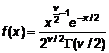
trong đó x > 0 và
với v > 0.
CHÚ THÍCH 1: Đối với dữ liệu phát sinh
từ phân bố chuẩn (2.50) có độ lệch chuẩn (2.37) σ đã biết,
thống kê nS2/σ2 có phân bố khi-bình phương với n
- 1
bậc
tự do. Kết quả này
là cơ sở để thu được
khoảng tin cậy đối với σ2. Lĩnh vực ứng dụng khác của
phân bố khi
bình
phương là như phân bố tham chiếu đối với sự phù hợp của phép kiểm nghiệm.
CHÚ THÍCH 2: Phân bố này là một trường
hợp đặc biệt của phân bố gamma (2.56) với các tham số α = v/2 và β
= 2. Tham số v được gọi là bậc
tự do (2.54).
CHÚ THÍCH 3: Trung
bình (2.35) của phân bố khi bình
phương là v. Phương
sai (2.36) của phân bố khi bình phương là 2v.
2.58
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26).
f(x) = β-1e-x/β
trong đó x > 0 và
tham số β
>
0.
CHÚ THÍCH 1: Phân bố mũ cung cấp cơ sở cho các ứng
dụng liên quan đến độ tin cậy, tương ứng với trường hợp “không bị lão hóa” hoặc
tính chất không có nhớ.
CHÚ THÍCH 2: Phân bố mũ là một trường
hợp đặc biệt của phân
bố gamma (2.56) với α = 1 hoặc tương đương phân bố khi bình
phương (2.57) với v = 2.
CHÚ THÍCH 3: Trung bình (2.35) của
phân bố mũ là β. Phương sai (2.36) của phân bố mũ là β2.
2.59
Phân bố beta
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
trong đó 0 ≤
x ≤
1
và với tham số α, β > 0.
CHÚ THÍCH: Phân bố beta rất linh hoạt,
có hàm
mật
độ xác suất có nhiều hình dạng
khác nhau “đơn
thức,
dạng chữ “j” dạng chữ “u”).
Phân bố này có thể sử
dụng như một mô hình của độ không đảm bảo đi kèm với một tỷ lệ. Ví dụ, trong
ứng dụng bảo hiểm bão, tỷ lệ hư hỏng mong muốn đối với một loại kết cấu với tốc
độ gió cho trước có thể là
0,40, mặc dù không phải gia đình nào gặp phải trường gió này cũng là do cùng loại hư
hại. Phân bố beta có trung bình 0,40 có thể dùng cho mô hình thiệt hại
không giống nhau theo loại kết cấu này.
2.60
Phân bố đều
Phân bố hình chữ nhật
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
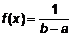
trong đó a ≤ x ≤
b.
CHÚ THÍCH 1: Phân bố đều với a
= 0 và b = 1 là phân bố cơ bản đối với bộ tạo số ngẫu nhiên điển hình.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 3: Phân bố đều là trường hợp
đặc biệt của phân bố beta với α = 1 và β = 1.
2.61
Phân bố cực
trị loại I
Phân bố Gumbel
Phân bố liên tục (2.23) có hàm
phân bố (2.7)
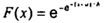
trong đó -∞ < x < ∞ với
các tham số -∞ < α < ∞, b >
0.
CHÚ THÍCH: Phân bố cực trị đưa ra phân
bố tham chiếu thích hợp cho các thống kê thứ tự (1.9) cực trị X(1) và X(n). Ba phân bố giới
hạn có thể khi n có xu hướng
tiến đến ∞ được đưa ra bởi ba loại phân bố cực trị nêu
trong 2.61,
2.62
và 2.63.
2.62
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phân bố Fréchet
Phân bố liên tục (2.23) có hàm
phân bố (2.7).
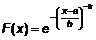
trong đó x > a và các tham
số -∞ < a < ∞, b
> 0, b
> 0, k > 0.
2.63
Phân bố cực
trị loại III
Phân bố Weibull
Phân bố liên tục (2.23) có
hàm phân bố (2.7)
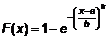
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Ngoài việc dùng làm một
trong ba phân bố giới hạn của thống kê thứ tự cực trị, phân bố Weibull chiếm
vị trí quan trọng trong các ứng dụng khác nhau, đặc biệt trong nghiên cứu độ
tin cậy và kỹ thuật. Phân bố Weibull đã chứng tỏ cung cấp tính phù hợp về thực nghiệm
cho nhiều loại tập dữ liệu khác nhau.
CHÚ THÍCH 2: Tham số a là tham số định
vị theo nghĩa là giá trị nhỏ nhất có thể có được trong phân bố Weibull. Tham
số b là tham số thang đo [liên quan đến độ lệch chuẩn (2.37) của
phân bố Weibull]. Tham
số k là tham số định dạng.
CHÚ THÍCH 3: Đối với k = 1,
phân bố Weibull có
dạng phân bố hàm mũ. Nâng lên phân bố mũ với a = 0 và tham số b
lên lũy thừa 1/k tạo thành
phân bố Weibull theo
định nghĩa. Một trường hợp đặc biệt khác của phân bố Weibull là phân bố
Rayleigh (với a = 0 và k = 2).
2.64
Phân bố chuẩn
nhiều chiều
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
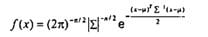
trong đó
-∞ < xi < ∞ đối với mỗi i;
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Σ là ma trận xác định dương, đối xứng n
x n
tham số; và
chữ đậm chỉ thị véctơ n
chiều.
CHÚ THÍCH: Mỗi phân bố biên duyên
(2.18) của phân bố nhiều chiều trong điều này có phân bố chuẩn. Tuy nhiên, có
nhiều phân bố nhiều chiều có phân bố biên duyên khác dạng phân bố nêu trong
điều này.
2.65
Phân bố chuẩn
hai chiều
Phân bố liên tục (2.23) có hàm
mật độ xác suất (2.26)
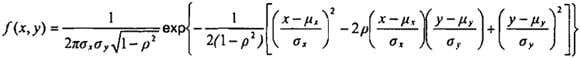
trong đó
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-∞ < y < ∞
-∞ < μx < ∞
-∞ < μy < ∞
σx > 0
σy > 0
|ρ| < 1
CHÚ THÍCH: Theo ký hiệu gợi ý, đối với
(X,Y) có hàm mật độ xác suất (2.26) nêu trên. E(X) = μx, E(Y)
= μy, V(X) = 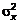 , V(Y) =
, V(Y) = 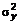 , và ρ là hệ số
tương quan (2.44) giữa X và Y.
, và ρ là hệ số
tương quan (2.44) giữa X và Y.
2.66
Phân bố chuẩn
chuẩn hóa hai chiều
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.67
Phân bố mẫu
Phân bố của một thống kê.
CHÚ THÍCH: Minh họa về phân bố mẫu cụ
thể được nêu trong chú
thích 1 của 2.53, chú thích 1 của 2.55 và chú thích 1 của 2.57.
2.68
Không gian
xác suất
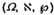
Không gian mẫu (2.1), và sigma
đại số của biến cố (2.69), và độ
đo xác suất (2.70).
VÍ DỤ 1: Một trường hợp đặc biệt,
không gian mẫu có thể chứa tất cả 105 cá thể sản xuất trong một ngày quy định
tại một nhà máy. Sigma đại số của biến cố gồm tất cả những tập con có thể. Các biến
cố này bao gồm {không có cá thể nào}, {cá thể 1}, {cá thể 2), ... {cá thể 105}, {cá thể 1 và cá thể
2}, .... {tất cả 105 cá thể}. Một thước đo xác suất có thể được xác định
là số cá thể trong một biến cố chia cho tổng số cá thể được sản xuất. Ví dụ, biến
cố {cá thể 4, cá thể 27, cá thể 92} có độ đo xác suất là 3/105.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.69
Sigma
đại số của biến cố
σ đại số
sigma trường
σ trường
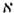
tập hợp các biến cố (2.2) có
tính chất:
a) thuộc 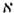 ;
;
b) Nếu một biến cố thuộc 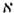 , thì biến cố bù
(2.3) cũng thuộc
, thì biến cố bù
(2.3) cũng thuộc  ;
;
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ 1: Nếu không gian mẫu là tập hợp các số
nguyên thì sigma đại số của biến cố có thể được chọn là tập hợp tất cả các tập
con của các số nguyên đó.
VÍ DỤ 2: Nếu không gian mẫu là tập hợp các số thực thì sigma đại số
của biến cố có thể được chọn bao gồm các tập hợp ứng với các khoảng trên đường
thẳng thực và tất cả các hợp vô hạn và đếm được cũng như giao của các khoảng
này. Có thể mở rộng ví dụ này ra số
chiều lớn hơn bằng cách xét “khoảng” k chiều. Cụ thể, với hai chiều, tập
hợp các khoảng có thể bao gồm các vùng xác định bởi {(x,y): x < s, y < t} đối với tất
cả các giá trị thực của s và t.
CHÚ THÍCH 1: Sigma đại số là tập hợp
bao gồm phần tử là các tập hợp. Tập hợp các kết quả Ω có thể có là phần
tử của
sigma đại số của biến cố, như chỉ ra trong tính chất a).
CHÚ THÍCH 2: Tính chất c)
liên quan đến tập hợp các phép tính trên các tập con (có thể là hữu hạn đếm được)
của sigma đại số của biến cố.
Ký hiệu được cho chỉ ra rằng tất cả các hợp đếm được và giao đếm được của các
tập hợp này cũng thuộc sigma đại số của biến cố.
CHÚ THÍCH 3: Tính chất c) bao hàm cả
tính khép kín (các tập hợp thuộc sigma đại số của biến cố) theo hợp hữu hạn
hoặc giao hữu hạn. Hạn định sigma được dùng để nhấn mạnh rằng A khép kín trong các
hợp hoặc giao vô hạn đếm được.
2.70
Độ đo xác
suất
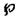
Hàm không âm xác định trên sigma đại số của
biến cố (2.69) sao cho
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
trong đó Ω biểu thị không
gian mẫu (2.1),
b) 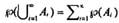
trong đó {Ai} là dãy các biến
cố (2.2) tách rời nhau đôi một.
VÍ DỤ: Tiếp theo ví dụ về pin ở
2.1, xét biến cố pin hoạt động ít hơn một giờ. Biến cố này gồm cặp các biến cố
tách rời {không hoạt
động} và {hoạt động ít
hơn một giờ nhưng hoạt động từ đầu}. Tương ứng, có thể biểu thị các biến cố {0} và
(0,1). Độ đo xác suất của {0} là tỷ lệ pin không hoạt động ngay từ lần đầu.
Độ đo xác suất của tập hợp (0, 1) phụ
thuộc vào xác suất phân bố liên tục cụ thể [ví dụ, phân bố mũ (2.58)] chi
phối phân bố hỏng.
CHÚ THÍCH 1: Độ đo xác suất ấn định
một giá trị từ [0, 1] đối với mỗi biến cố trong sigma đại số của biến cố. Giá
trị 0 ứng với biến cố không thể xảy ra, trong khi giá trị 1 biểu diễn khả năng chắc chắn
xảy ra. Cụ thể, độ đo xác suất của tập trống bằng không và độ đo xác suất ấn
định cho không gian mẫu là 1.
CHÚ THÍCH 2: Tính chất b) chỉ
ra rằng nếu dãy các biến cố không có phần chung khi xét theo cặp thì độ đo xác
suất của hợp các biến cố đó là tổng các độ đo xác suất đơn lẻ. Để chỉ rõ thêm cho
tính chất b), nếu số biến cố là vô hạn đếm được thì điều này vẫn đúng.
CHÚ THÍCH 3: Ba thành phần của xác
suất có liên hệ thông qua các biến ngẫu nhiên. Xác suất (2.5) của các biến cố
trong tập ảnh của biến ngẫu nhiên (2.10) tính được từ xác suất của biến
cố trong không gian mẫu. Biến cố trong tập ảnh của biến ngẫu nhiên được ấn định
xác suất của biến cố trong không gian mẫu chiếu lên nó bằng biến ngẫu nhiên.
CHÚ THÍCH 4: Tập ảnh của biến ngẫu nhiên
là tập số thực hoặc bộ n số thực. (Chú ý tập ảnh là tập hợp mà biến ngẫu
nhiên chiếu lên đó.)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
(tham khảo)
Ký hiệu
Ký hiệu
Symbol(s)
Thuật ngữ
Tiếng việt
Vietnamese
term
Thuật ngữ
tiếng Anh
English term
Số điều
Term
No.
A
biến cố
event
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
AC
biến cố bù
complementary event
2.3
sigma đại số của biến cố, σ đại số,
sigma trường
σ -trường
sigma algebra of events, σ algebra,
sigma field
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.69
α
mức ý nghĩa
significance level
1.45
α, λ, μ, β, σ, ρ, γ, p, N, M, c,
v, a, b, k
tham số
parameter
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hệ số nhọn
coefficient of kurtosis
2.40
E(Xk)
mômen mẫu bậc k
sample moment of order k
1.14
E[g(X)]
kỳ vọng của hàm g của biến
ngẫu nhiên X
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.12
F(x)
hàm phân bố
distribution function
2.7
f(x)
hàm mật độ xác suất
probability density function
2.26
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hệ số bất đối xứng
coefficient of skewness
2.39
H
giả thuyết
hypothesis
1.40
H0
giả thuyết không
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.41
HA, H1
đối giả thuyết
alternative hypothesis
1.42
k
số chiều
dimension
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
bậc của mômen
order of a moment
1.14, 2.34,
2.41, 2.42
μ
trung bình
mean
2.35
v
bậc tự do
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.54
n
cỡ mẫu
sample size
&
không gian mẫu
sample space
2.1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
không gian xác suất
probability space
2.68
P(A)
xác suất của biến cố A
probability of an event A
2.5
P(A\B)
xác suất có điều kiện của A
cho trước B
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.6
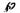
độ đo xác suất
probability measure
2.70
rxy
hệ số tương quan mẫu
sample correlation coefficient
1.23
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
giá trị quan trắc của độ lệch chuẩn
mẫu
observed value of a samplestandard deviation
S
độ lệch chuẩn mẫu
sample standard
deviation
1.17
S2
phương sai mẫu
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.16
SXY
hiệp phương sai mẫu
sample covariance
1.22
σ
độ lệch chuẩn
standard deviation
2.37
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phương sai
variance
2.36
σXY
hiệp phương sai
covariance
2.43
sai số tiêu chuẩn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.24
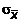
sai số tiêu chuẩn của trung bình mẫu
standard error of the sample mean
θ
tham số của phân bố
parameter of a
distribution
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hàm ước lượng
estimator
1.12
V(X)
phương sai của biến ngẫu nhiên X
variance of a random variable X
2.36
X(i)
thống kê thứ tự i
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.9
x, y, z
giá trị quan trắc
observed value
1.4
X, Y, Z, T
biến ngẫu nhiên
random variable
2.10
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
p phân vị
p-quantile
2.13
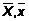
trung bình, trung bình mẫu
average, sample mean
1.15
Phụ
lục B
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Sơ đồ khái niệm thống kê
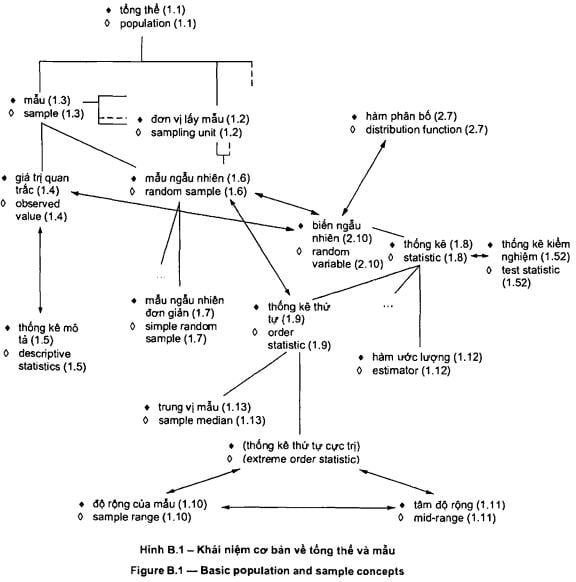
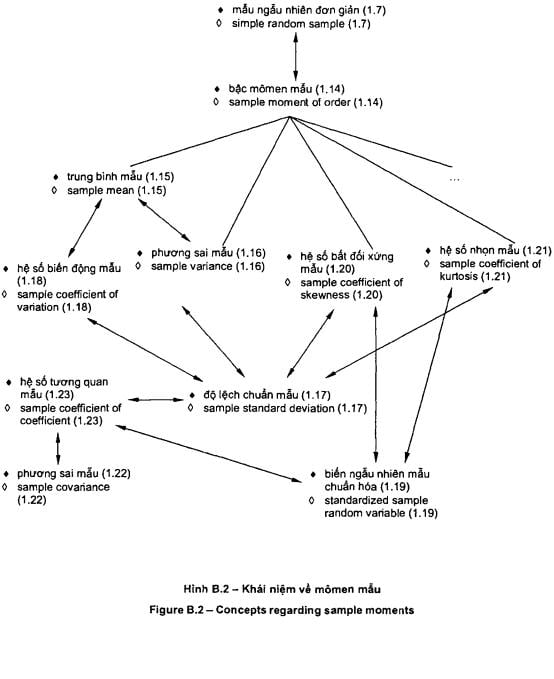

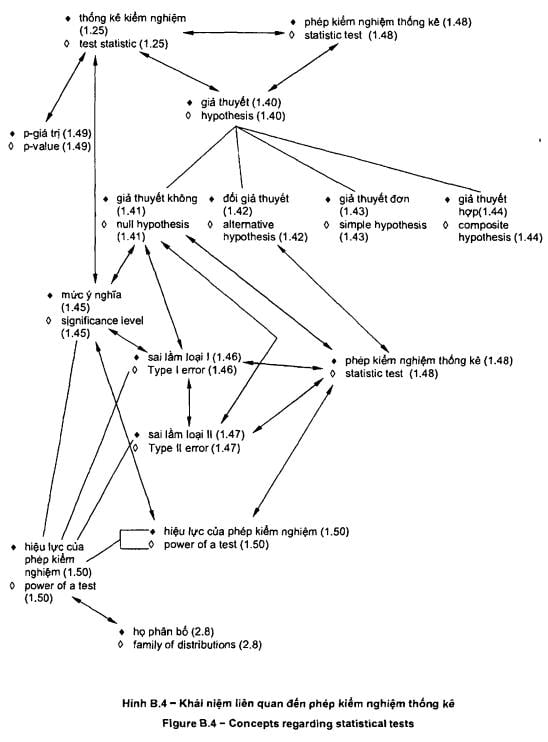
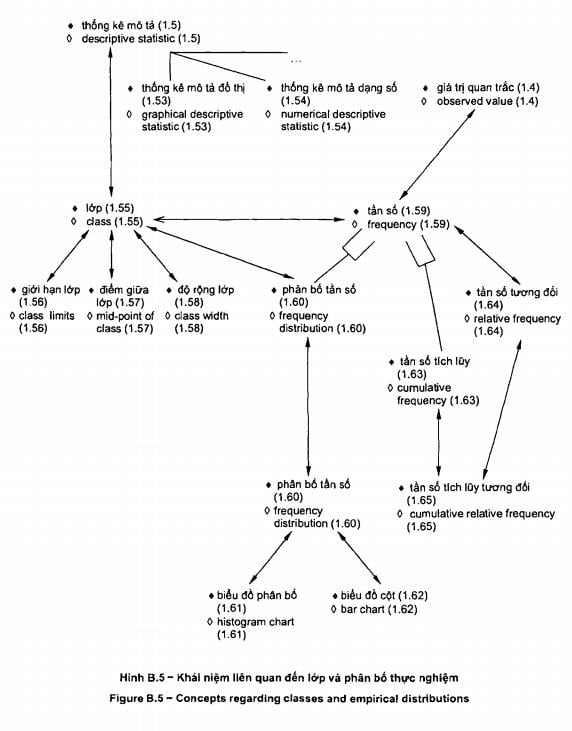
Phụ
lục C
(tham khảo)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Annex C
(informative)
Probability
concept diagrams
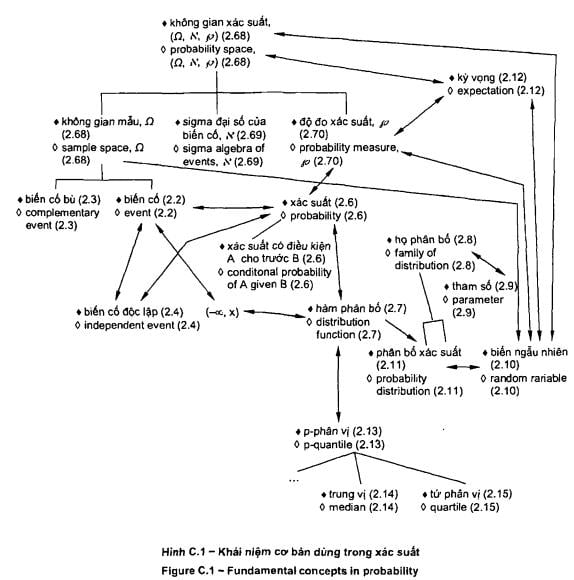
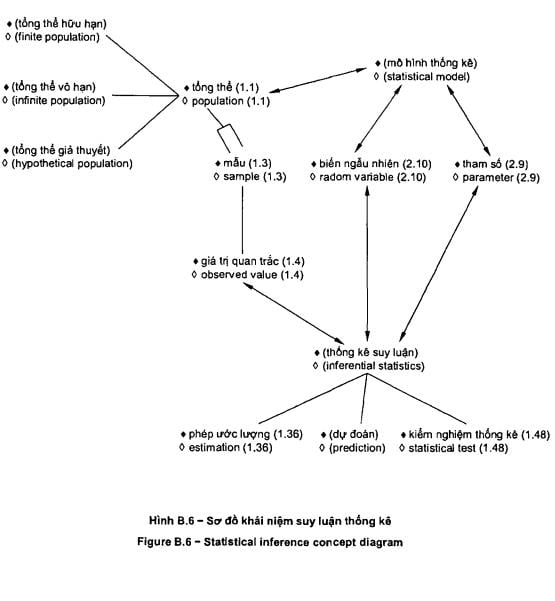
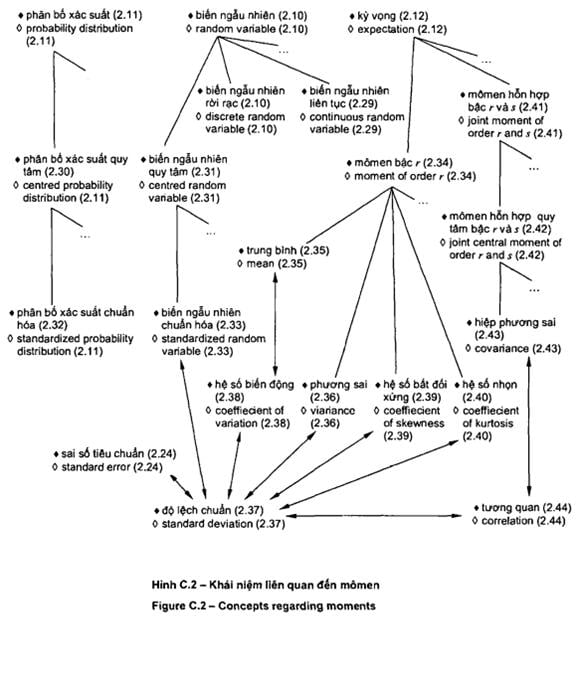


...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ
lục D
(tham khảo)
Phương pháp luận sử dụng khi xây dựng từ vựng
D.1 Giới thiệu
Ứng dụng phổ biến của bộ tiêu chuẩn này đòi hỏi phải sử dụng bộ từ
vựng chặt chẽ và hài hòa sao cho những người sử dụng các tiêu chuẩn thống kê
ứng dụng hiểu được một cách dễ dàng.
Các khái niệm đều có liên quan đến
nhau và việc phân tích mối quan hệ giữa các khái niệm trong lĩnh vực thống kê
ứng dụng cũng như sắp xếp chúng theo các sơ đồ khái niệm là điều tiên quyết đối
với một bộ từ vựng chặt chẽ. Phân tích này được sử dụng khi xây dựng tiêu chuẩn
này. Vì sơ đồ khái niệm sử dụng trong quá trình xây dựng từ vựng có thể hữu ích
cho việc tham khảo nên các sơ đồ đã được nhắc lại trong D.4.
D.2 Nội dung mục
từ vựng và quy tắc thay thế
Khái niệm là đơn vị chuyển đổi giữa các
ngôn ngữ (bao gồm cả những khác biệt trong một ngôn ngữ, ví dụ như tiếng Anh Mỹ
và tiếng Anh Anh). Đối với mỗi ngôn ngữ, thuật ngữ thích hợp nhất cho tính rõ
ràng phổ dụng của khái niệm ở ngôn ngữ đó, nghĩa là không phải một bản dịch, sẽ
lựa được chọn.
Định nghĩa hình thành bởi việc mô tả chỉ những
đặc trưng thiết yếu để nhận biết khái niệm. Thông tin liên quan đến khái niệm
cũng quan trọng nhưng không cần thiết cho việc mô tả khái niệm được đặt trong
một hoặc nhiều chú thích kèm theo định nghĩa.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
D.3 Mối quan hệ của
khái niệm và việc thể hiện chúng bằng sơ đồ
B.3.1 Khái quát
Trong thuật ngữ học, ở chừng mực có
thể, mối quan hệ giữa các khái niệm được dựa trên thông tin thứ bậc về đặc
trưng của loại sao cho mô tả ngắn gọn nhất khái niệm bằng cách gọi
tên loại của nó và mô tả đặc trưng phân biệt nó với các khái niệm mẹ hoặc anh em.
Có ba dạng quan hệ khái niệm chính
được nêu trong phụ lục này: chung (D.3.2), bộ phận (D.3.3) và liên kết (D.3.4).
D.3.2 Mối quan hệ
chung
Các khái niệm phụ trong hệ thống thứ
bậc kế thừa tất cả các đặc trưng của khái niệm chính và bao gồm mô tả
về các đặc trưng này để phân biệt chúng với các khái niệm gốc (mẹ) và ngang
bằng (anh em), ví dụ quan hệ giữa xuân, hè, thu và đông với mùa.
Mối quan hệ chung được mô tả bằng một
sơ đồ quạt hoặc cây không có mũi tên (xem Hình D.1).
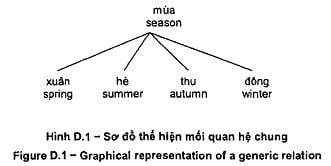
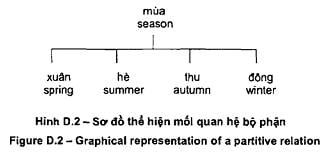
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Các khái niệm phụ trong một
hệ thống thứ bậc tạo thành các bộ phận cấu thành của khái niệm chính, ví dụ
xuân, hạ, thu và đông có thể được xác định là bộ phận của khái niệm năm. Khi so
sánh, sẽ không thích hợp nếu định nghĩa thời tiết nắng (một đặc trưng của mùa
hè) là bộ phận của năm.
Mối quan hệ thành phần được mô tả bằng
hình cái cào, không
có mũi tên (xem Hình D.2). Các bộ phận số ít được mô tả bằng một đường thẳng,
các bộ phận số nhiều được mô tả bằng hai đường thẳng.

D.3.4 Mối quan hệ
liên kết
Mối quan hệ liên kết không thể đưa ra
mô tả ngắn gọn như trong mối quan hệ chung và quan hệ bộ phận nhưng nó rất hữu
ích cho việc xác định bản chất mối quan hệ giữa các khái niệm trong một hệ
thống khái niệm, ví dụ: nguyên nhân và kết quả, hoạt động và vị trí, hoạt động
và kết quả, công cụ và chức năng, vật liệu và sản phẩm.
Mối quan hệ liên kết được mô tả bằng
đường thẳng có mũi tên ở hai đầu (xem hình D.3).

D.4 Sơ đồ khái
niệm
Các hình từ B.1 đến B.5 thể hiện sơ đồ
khái niệm là cơ sở của các định nghĩa trong điều 1 của tiêu chuẩn này. Hình B.6
là sơ đồ khái niệm bổ sung chỉ ra mối quan hệ giữa các thuật ngữ nhất định
trước đó được đề cập trong các hình từ B.1 đến B.5. Các hình từ C.1 đến C.4 thể
hiện sơ đồ khái niệm là cơ sở của các định nghĩa trong điều 2 của tiêu chuẩn
này. Có nhiều thuật ngữ xuất hiện trong nhiều sơ đồ khái niệm được đưa ra, cung
cấp mối liên kết giữa các sơ đồ. Điều này được chỉ ra như sau:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
thống kê mô tả (1.5)
Hình B.5
mẫu ngẫu nhiên đơn giản (1.7)
Hình B.2
hàm ước lượng (1.12)
Hình B.3
thống kê kiểm nghiệm (1.52)
Hình B.4
biến ngẫu nhiên (2.10)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hàm phân bố (2.7)
Hình C.1
Hình B.2 Khái niệm liên quan đến
mômen mẫu:
mẫu ngẫu nhiên đơn giản (1.7)
Hình B.1
Hình B.3 Khái niệm ước lượng:
hàm ước lượng (1.12)
Hình B.1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình C.1
họ phân bố (2.8)
Hình B.4, C.1
hàm mật độ xác suất
(2.26)
Hình C.3
hàm khối lượng xác suất (2.24)
Hình C.3
Hình B.4 Khái niệm liên quan đến
phép kiểm nghiệm thống kê:
thống kê kiểm nghiệm (1.52)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hàm mật độ xác suất (2.26)
Hình B.3, C.3
hàm khối lượng xác suất (2.24)
Hình B.3, C.3
họ phân bố (2.8)
Hình B.3, C.1
Hình B.5 Khái niệm liên quan đến lớp
và phân bố thực nghiệm:
thống kê mô tả (1.5)
Hình B.1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
tổng thể (1.1)
Hình B.1
mẫu (1.3)
Hình B.1
giá trị quan trắc (1.4)
Hình B.1, B.5
phép ước lượng (1.36)
Hình B.3
kiểm nghiệm thống kê (1.48)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
tham số (2.9)
Hình B.3, C.1
biến ngẫu nhiên (2.10)
Hình B.1, C.1, C.2
Hình C.1 Khái niệm cơ bản dùng
trong xác suất:
biến ngẫu nhiên (2.10)
Hình B.1, C.2
phân bố xác suất (2.11)
Hình C.2, C.3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình B.3, B.4
hàm phân bố (2.7)
Hình B.1
tham số (2.9)
Hình B.3
Hình C.2 Khái niệm mômen:
biến ngẫu nhiên (2.10)
Hình B.1, C.1
phân bố xác suất (2.11)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình C.3 Khái niệm phân bố xác suất:
phân bố xác suất (2.11)
Hình C.1, C.2
hàm khối lượng xác suất
(2.24)
Hình B.3, B.4
phân bố liên tục (2.23)
Hình C.4
phân bố một chiều (2.16)
Hình C.4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình C.4
Hình C.4 Khái niệm
liên quan đến phân bố liên tục:
phân bố một chiều (2.16)
Hình C.3
phân bố nhiều chiều (2.17)
Hình C.3
phân bố liên tục (2.23)
Hình C.3
Chú thích cuối của Hình C.4, các phân bố dưới
đây là ví dụ của phân bố một chiều: phân bố chuẩn, phân bố t, phân bố F,
phân bố chuẩn chuẩn hóa, phân bố gamma, beta, khi-bình phương, mũ, đều, cực trị
loại I, cực trị loại II và cực trị loại III. Các phân bố dưới đây là ví dụ của
phân bố nhiều chiều: phân bố chuẩn đa biến, phân bố chuẩn hai biến và phân bố
chuẩn chuẩn hóa hai biến. Việc đưa thêm phân bố đơn biến (2.16) và phân bố đa
biến (2.17) vào sơ đồ khái niệm có thể làm cho hình trở nên rắc rối quá mức.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
[1] TCVN 6398-11:199 , Đại lượng và
đơn vị - Phần 11: Dấu và ký hiệu toán học dùng trong khoa học vật lý và công
nghệ
[2] TCVN 8244-1, Thống kê học - Từ
vựng và ký
hiệu
- Phần 2: Thống kê ứng dụng
[3] TCVN 6910 (tất cả các
phần), Độ chính xác (độ đúng và độ
chụm) của phương pháp đo và kết quả đo
[4] TCVN 6165, Từ vựng quốc tế về đo lường học -
Khái niệm, thuật ngữ chung và cơ bản (VIM)
Chỉ mục theo bảng chữ cái
phân bố X2
2.57
σ-đại số 2.69
σ-trường 2.69
B
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
biến cố bù 2.3
biến cố độc lập 2.4
biến cố 2.2
biên giới lớp 1.56
biến ngẫu nhiên
chuẩn hóa
2.33
biến ngẫu nhiên
liên tục
2.29
biến ngẫu nhiên mẫu
chuẩn hóa
1.19
biến ngẫu nhiên quy
tâm
2.31
biến ngẫu nhiên rời
rạc 2.28
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
biểu đồ cột 1.62
biểu đồ phân bố 1.61
Đ
điểm giữa lớp 1.57
độ chệch 1.33
độ đo xác suất 2.70
độ lệch chuẩn 2.37
độ lệch chuẩn mẫu 1.17
độ rộng lớp 1.58
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
đối giả thuyết 1.42
đơn vị mẫu 1.2
đường hiệu lực 1.51
đường hồi quy 2.20
G
giả thuyết đơn 1.43
giả thuyết hợp 1.44
giả thuyết không 1.41
giả thuyết 1.40
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
giới hạn dung sai
thống kê
1.27
giới hạn lớp 1.56
H
hàm hợp lý 1.38
hàm hợp lý biên
duyên
1.39
hàm khái lượng xác
suất
2.24
hàm mật độ xác suất 2.26
hàm phân bố của
biến ngẫu nhiên X 2.7
phương sai mẫu 1.16
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
p-phân vị 2.13
S
sai lầm loại I 1.46
sai lầm loại II 1.47
sai số của phép ước
lượng
1.32
sai số tiêu chuẩn 1.24
sigma đại số của
biến cố
2.69
sigma trường 2.69
T
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
tần số 1.59
tần số tích lũy 1.63
tần số tích lũy
tương đối
1.65
tần số tương đối 1.64
tham số 2.9
thống kê kiểm
nghiệm
1.52
thống kê mô tả 1.5
thống kê mô tả dạng
số
1.54
thống kê mô tả đồ
thị
1.53
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
thống kê 1.8
tổng thể 1.1
trung bình 1.15,
2.35.1, 2.35.2
trung bình mẫu 1.15
trung bình số học 1.15
trung bình 1.15
trung vị 2.14
trung vị mẫu 1.13
hàm ước lượng 1.12
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hệ số bất đối xứng 2.39
hệ số bất đối xứng
mẫu
1.20
hệ số biến động 2.38
hệ số biến động mẫu 1.18
hệ số nhọn 2.40
hệ số nhọn mẫu 1.21
hệ số tương quan 2.44
hệ số tương quan
mẫu
1.23
hiệp phương sai 2.43
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hiệu lực của phép
kiểm nghiệm
1.50
họ phân bố 2.8
K
khoảng dự đoán 1.30
khoảng dung sai
thống kê
1.26
khoảng tin cậy một
phía
1.29
khoảng tin cậy 1.28
không gian mẫu 2.1
không gian xác suất 2.68
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
kiểm nghiệm thống
kê
1.48
kỳ vọng 2.12
L
lớp 1.55
lớp 1.55.1,
1.55.2, 1.55.3
M
mặt hồi quy 2.21
mẫu ngẫu nhiên đơn
giản
1.7
mẫu ngẫu nhiên 1.6
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
mômen bậc r 2.34
mômen bậc r =
1 2.35.1
mômen hỗn hợp bậc r và
s 2.41
mômen hỗn hợp quy
tâm bậc r và s
2.42
mômen mẫu bậc k 1.14
mômen thứ r 2.34
mốt của hàm khối
lượng xác suất 2.25
mốt của hàm mật độ
xác suất
2.27
mức ý nghĩa 1.45
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
ước lượng 1.31
ước lượng khoảng 1.25
ước lượng không
chệch
1.34
X
xác suất có điều
kiện
2.6
xác suất của biến
cố A
2.5
P
p-giá trị 1.49
phân bố 2.11
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phân bố biên duyên 2.18
phân bố chuẩn 2.50
phân bố chuẩn chuẩn
hóa hai chiều 2.66
phân bố chuẩn chuẩn
hóa
2.51
phân bố chuẩn đa
biến
2.64
phân bố chuẩn hai
biến
2.65
phân bố có điều
kiện
2.19
phân bố I cực trị
loại I
2.61
phân bố cực trị
loại II
2.62
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phân bố đa thức 2.45
phân bố đều 2.60
phân bố F 2.55
phân bố Fréchet 2.62
phân bố gamma 2.56
phân bố Gausslan 2.50
phân bố Gaussian
chuẩn hóa
2.51
phân bố Gumbel 2.61
phân bố hình chữ
nhật
2.60
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phân bố liên tục 2.23
phân bố lôga chuẩn 2.52
phân bố mẫu 2.67
phân bố một chiều 2.16
phân bố mũ 2.58
phân bố nhị thức âm 2.49
phân bố nhị thức 2.46
phân bố nhiều chiều 2.17
phân bố Poisson 2.47
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phân bố siêu hình
học
2.48
phân bố Student 2.53
phân bố t
2.53
phân bố tần số 1.60
phân bố Weibull 2.63
phân bố xác suất
biên duyên
2.18
phân bố xác suất
chuẩn hóa
2.32
phân bố xác suất có
điều kiện
2.19
phân bố xác suất đa
biến
2.17
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
phân bố xác suất
liên tục
2.23
phân bố xác suất
quy tâm
2.30
phân bố xác suất
rời rạc
2.22
phân bố xác suất 2.11
phân vị 2.15
phép ước lượng 1.36
phép ước lượng hợp
lý cực đại
1.37
