TIÊU CHUẨN QUỐC
GIA
TCVN
12741:2019
ISO/TS 28037:2010
XÁC
ĐỊNH VÀ SỬ DỤNG HÀM HIỆU CHUẨN ĐƯỜNG THẲNG
Determination
and use of straight-line calibration functions-
Lời nói đầu
TCVN 12741:2019 hoàn toàn tương đương
với ISO/TS 28037:2010.
TCVN 12741:2019 do Ban kỹ thuật tiêu
chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng
cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Lời giới thiệu
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Với thông tin độ không đảm bảo kèm
theo dữ liệu đo, phương pháp thích hợp có thể được quy định để xác định các ước lượng
của tham số hàm
hiệu chuẩn. Thông tin về độ không đảm bảo này có thể bao gồm hiệu ứng hiệp
phương sai định lượng, liên quan đến sự phụ thuộc giữa một số hoặc tất cả các đại
lượng liên quan.
Khi mô hình đường thẳng đã được khớp với
dữ liệu, cần xác định xem mô hình và dữ liệu có thống nhất với nhau hay không.
Trong trường hợp thống nhất, mô hình thu được có thể sử dụng để dự đoán giá trị
x của biến X tương ứng với giá trị đo được y của biến Y
cung cấp bởi cùng một hệ
thống đo. Cũng có thể sử dụng mô hình này để đánh giá độ không đảm bảo kèm theo
các tham số hàm hiệu chuẩn và độ không đảm bảo kèm theo giá trị dự đoán x.
Do đó, việc xác định và sử
dụng hàm hiệu chuẩn đường thẳng có thể được xem là gồm năm bước:
1
Thu thập thông tin về độ không đảm
bảo và hiệp phương sai gắn với dữ liệu đo - mặc dù phụ thuộc vào lĩnh vực đo
cụ thể, các ví dụ được cung cấp trong tiêu chuẩn này;
2
Cung cấp ước lượng tốt nhất của các
tham số đường thẳng;
3
Xác định giá trị sử dụng của mô
hình, cả về dạng chức năng (dữ liệu có phản ánh mối quan hệ đường thẳng
không"?) và về mặt thống kê (độ trải của dữ liệu có nhất quán
với độ không đảm bảo kèm theo của chúng không?) bằng cách sử dụng kiểm nghiệm
Khi-bình phương;
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Thu được độ không đảm bảo chuẩn và
hiệp phương sai gắn với ước lượng của các tham số đường thẳng;
5
Sử dụng hàm hiệu chuẩn để dự đoán, tức
là, xác định ước lượng x của biến X và độ không đảm bảo
kèm theo tương ứng với giá trị đo được y của biến Y và độ
không đảm bảo kèm theo.
Các bước trên đây được trình bày bằng
sơ đồ trên Hình 1.
Mục đích chính của tiêu
chuẩn này là để xem xét
các bước từ 2 đến 5. Do đó, như một phần bước 1, trước khi sử dụng tiêu
chuẩn này, người sử dụng sẽ cần
cung cấp độ không đảm bảo chuẩn, và hiệp phương sai nếu liên quan, gắn với giá
trị Y đo được và, khi thích hợp, độ không đảm bảo chuẩn, và hiệp phương
sai nếu liên quan, gắn với giá trị X đo được, Cần tính đến
các nguyên tắc của GUM khi đánh giá độ không đảm bảo này dựa
trên mô hình đo cụ thể cho lĩnh vực liên quan.
TCVN 9598:2013 (ISO 11095:1996) [14]
liên quan đến hiệu chuẩn tuyến tính sử dụng mẫu chuẩn. Những khác biệt so với tiêu
chuẩn này được trình bày trong Bảng 1.
Phương pháp số được cho dựa trên Tài
liệu tham khảo [6].

Hình 1 - Tóm tắt các
bước trong việc xác định và sử dụng hàm hiệu chuẩn đường thẳng
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Đặc điểm
TCVN 9598:2013 (ISO 11095:1996)
Tiêu chuẩn này
Đề cập cụ thể đến mẫu chuẩn
Có
Tổng quát hơn
X-giá trị giả định là biết chính
xác
Có
Thông tin độ không đảm bảo chung hơn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Có
Thông tin độ không đảm bảo chung hơn
Thuật ngữ thống nhất với GUM
Không
Có
Số kiểu cấu trúc độ không đảm bảo được
xử lý
Hai
Năm, bao gồm trường hợp tổng quát nhất
Chỉ độ không đảm bảo gắn với
sai số ngẫu nhiên
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Thông tin độ không đảm bảo tổng quát
hơn
Kiểm nghiệm tính nhất quán
ANOVA
Khi-bình phương
Độ không đảm bảo gắn với các dự đoán
Đặc biệt
Tương thích với GUM
XÁC ĐỊNH VÀ SỬ
DỤNG HÀM HIỆU CHUẨN ĐƯỜNG THẲNG
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1 Phạm vi áp dụng
Tiêu chuẩn này đề cập đến hàm hiệu chuẩn
tuyến tính, tức hàm hiệu chuẩn đường thẳng, mô tả mối quan hệ giữa hai biến X
và Y, gọi là hàm có dạng Y = A + BX. Mặc dù có nhiều nguyên tắc
áp dụng cho các loại hàm hiệu chuẩn tổng quát hơn, nhưng bất kỳ khi nào có thể,
các cách tiếp cận được mô tả đều khai thác dạng đơn giản của hàm hiệu chuẩn đường
thẳng.
Giá trị của các tham số A và B,
được xác định trên cơ sở các điểm dữ
liệu đo được (xi,
yi), i =
1,…, m. Nhiều trường
hợp khác nhau được xem xét liên quan đến tính chất của độ không đảm bảo kèm
theo các dữ liệu này. Không có giả định nào được đưa ra về sai số liên quan đến yi là phương
sai không đổi (có phương sai bằng nhau), và tương tự với xi khi sai số
là đáng kể.
Ước lượng của các tham số A và B được xác định
bằng cách sử dụng phương pháp bình phương tối thiểu. Điểm nhấn mạnh của tiêu chuẩn
này là việc chọn phương pháp bình phương tối thiểu thích hợp nhất cho loại dữ liệu đo, cụ
thể là các phương pháp phản ánh độ không đảm bảo kèm theo. Loại ma trận hiệp
phương sai tổng quát nhất gắn với dữ liệu đo được xử lý, nhưng những trường hợp
đặc biệt quan trọng dẫn đến các tính toán đơn giản hơn sẽ được mô tả chi tiết.
Đối với tất cả các trường hợp
xem xét, phương pháp xác nhận việc sử dụng hàm hiệu chuẩn đường thẳng và đánh
giá độ không đảm bảo, hiệp phương sai kèm theo các ước lượng tham số sẽ được
đưa ra.
Tiêu chuẩn này cũng mô tả việc sử dụng
các ước lượng tham số của hàm hiệu chuẩn và độ không đảm bảo, hiệp phương sai
kèm theo của chúng để dự đoán giá
trị của X và độ không đảm bảo chuẩn kèm theo dựa vào giá trị đo được của Y
và độ không đảm bảo chuẩn kèm theo.
CHÚ THÍCH 1: Tiêu chuẩn này không
đưa ra cách xử lý chung các giá trị bất thường trong dữ liệu đo, mặc dù kiểm
nghiệm hiệu lực đã cho có thể sử dụng làm cơ sở để xác định dữ liệu không thống nhất.
CHÚ THÍCH 2: Tiêu chuẩn này mô tả phương
pháp đánh giá độ không đảm bảo gắn với dữ liệu đo trong trường hợp độ không đảm
bảo chỉ được biết dựa
vào hệ số thang đo (Phụ lục E).
2 Tài liệu viện dẫn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
TCVN 6165:2009 (ISO/IEC Guide
99:2007), Từ vựng quốc tế về đo lường học - Khái niệm, thuật ngữ chung và cơ bản
(VIM)
TCVN 9595-3:2013 (ISO/IEC Guide
98-3:2008), Độ không đảm bảo đo - Phần 3: Hướng dẫn trình bày độ
không đảm bảo đo (GUM:1995)
3 Thuật ngữ và định
nghĩa
Tiêu chuẩn này áp dụng các thuật ngữ
và định nghĩa trong TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008), TCVN 6165:2009
(ISO/IEC Guide 99:2007) và các thuật ngữ và định nghĩa dưới đây.
Giải thích các ký hiệu chính được nêu
trong Phụ lục G.
3.1
Giá trị đại lượng đo được (measured
quantity value)
Giá trị đại lượng đại diện cho kết quả
đo.
[TCVN 6165:2009 (ISO/IEC Guide
99:2007), 2.10]
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Độ không đảm bảo đo (measurement
uncertainty)
Tham số không âm đặc trưng cho sự phân
tán của các giá trị đại lượng được quy cho đại lượng đo, trên cơ sở thông tin
đã sử dụng.
[TCVN 6165:2009 (ISO/IEC Guide
99:2007), 2.26]
3.3
Độ không đảm bảo đo chuẩn (standard
measurement uncertainty)
Độ không đảm bảo đo được thể hiện là độ
lệch chuẩn.
[TCVN 6165:2009 (ISO/IEC Guide
99:2007), 2.30]
3.4
Hiệp phương sai gắn với hai giá trị đại
lượng
(covariance associated with two quantity values)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.5
Ma trận hiệp phương sai đo (measurement
covariance matrix)
Ma trận hiệp phương sai (covariance
matrix)
Ma trận kích thước N x N gắn với ước
lượng véc tơ của đại lượng véc tơ kích thước N x 1, chứa trên đường
chéo của nó các bình phương của độ không đảm bảo chuẩn gắn với các thành phần
tương ứng của ước lượng véc tơ của đại lượng véc tơ, và, trên các vị trí ngoài
đường chéo của nó, là các hiệp phương sai gắn với các cặp thành phần của ước lượng
véc tơ của đại lượng véc tơ.
CHÚ THÍCH 1: Ma trận hiệp phương sai Ux
kích thước N x N gắn với ước lượng véc tơ x của
đại lượng véc tơ X
có dạng

trong đó cov(xi, xj) = u2(xi)
là phương sai (độ không đảm bảo chuẩn
bình phương) gắn với xi và cov(xi, xj) là hiệp
phương sai gắn với xi và xj. cov(xi, xj) = 0 nếu các
thành phần Xi và Xj, của X
là không tương quan.
CHÚ THÍCH 2: Các hiệp phương sai còn gọi là độ
không đảm bảo tương hỗ.
CHÚ THÍCH 3: Ma trận hiệp phương sai
còn gọi là ma trận
phương sai-hiệp phương sai.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.6
Mô hình đo (measurment model)
Hệ thức toán học trong đó tất cả các đại
lượng đã biết liên quan đến phép đo.
[TCVN 6165:2009 (ISO/IEC Guide
99:2007), 2.48]
3.7
Mô hình hàm (functional model)
Mô hình thống kê liên
quan đến các sai số gắn với biến phụ thuộc.
3.8
Mô hình cấu trúc (structural
model)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.9
Hiệu chuẩn (calibration)
Hoạt động, trong những điều kiện quy định,
bước thứ nhất là thiết lập mối liên hệ giữa các giá trị đại lượng có độ không đảm
bảo đo do chuẩn đo lường cung cấp và các số chỉ tương ứng với độ không đảm bảo
đo kèm theo và bước thứ hai là sử dụng thông tin này thiết lập mối liên hệ để
nhận được kết quả đo từ số chỉ.
CHÚ THÍCH 1: Hiệu chuẩn có thể diễn tả
bằng một tuyên bố, hàm hiệu chuẩn, biểu đồ hiệu chuẩn, đường cong
hiệu chuẩn, hoặc bảng hiệu chuẩn. Trong một số trường hợp nó có thể bao gồm sự
hiệu chính cộng hoặc nhân của số chỉ với độ không đảm bảo đo kèm theo.
CHÚ THÍCH 2: Không được nhầm lẫn hiệu
chuẩn với hiệu chỉnh hệ thống đo, thường gọi sai là “tự hiệu chuẩn”, cũng không
được nhầm lẫn với kiểm định của hiệu chuẩn.
CHÚ THÍCH 3: Thông thường chỉ
riêng bước đầu tiên trong định nghĩa trên được hiểu là hiệu chuẩn.
[TCVN 6165:2009 (ISO/IEC Guide
99:2007), 2.39]
3.10
Phân bố xác suất (probability
distribution)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 1: Xác suất trên toàn bộ tập
hợp giá trị của biến ngẫu nhiên bằng 1.
CHÚ THÍCH 2: Phân bố xác suất được gọi
là đơn biến khi nó liên quan đến một biến ngẫu nhiên (vô hướng), và đa biến khi
nó liên quan đến véc tơ của các biến ngẫu nhiên. Phân bố xác suất đa biến còn
được mô tả là phân bố đồng thời.
CHÚ THÍCH 3:
Phân bố xác suất có thể có dạng hàm
phân bố hoặc hàm mật độ xác suất.
CHÚ THÍCH 4: Định nghĩa và Chú thích 1
lấy từ TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.11 và TCVN 9595-3:2013
(ISO/IEC Guide 98-3:2008), định nghĩa C.2.3; Chú thích 2 và 3 lấy từ ISO/IEC Guide 98-3:2008/Suppl.
1:2008, định nghĩa 3.1 [13].
3.11
Phân bố chuẩn (normal
distribution)
Phân bố xác suất của biến ngẫu nhiên
liên tục X có hàm mật độ xác suất

với -∞ < x < +∞
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Phân bố chuẩn còn được
gọi là phân bố Gauss.
CHÚ THÍCH 3: Định nghĩa và Chú thích 1 lấy
từ TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.50; Chú thích 2 lấy từ TCVN
9595-3:2013 (ISO/IEC Guide 98-3:2008), định nghĩa C.2.14.
3.12
Phân bố t
(t-distribution)
Phân bố xác suất của biến ngẫu nhiên
liên tục X có hàm mật độ xác suất

với -∞ < x
< +∞,
với tham số v, số nguyên dương, là bậc tự do của phân bố, trong đó

là hàm gamma.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.13
Phân bố Khi-bình phương (chi-squared
distribution)
Phân bố c2 (c2 distribution)
Phân bố xác suất của biến ngẫu nhiên
liên tục
X có hàm mật độ
xác suất

với 0 ≤ x < +∞, với tham số v, số nguyên
dương, trong đó  là
hàm gamma.
là
hàm gamma.
CHÚ THÍCH: Tổng bình phương của
n biến chuẩn chuẩn hóa độc
lập là biến ngẫu nhiên c2 với tham số n; khi đó n được gọi là bậc tự
do.
3.14
Ma trận xác định dương (positive
definite matrix)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.15
Ma trận nửa xác định dương (positive
semi-definite matrix)
Ma trận M kích thước n x n có tính chất zTMz ≥ 0 đối với mọi véc
tơ z khác 0 kích thước n x 1.
4 Quy ước và ký hiệu
Với mục đích của tiêu chuẩn này, các
quy ước và ký hiệu sau được sử dụng.
4.1 X được
gọi là biến độc lập và Y là biến phụ thuộc ngay cả khi hiểu biết về X
và Y là ‘có thể hoán đổi’ ví dụ như trong Điều 7.
4.2 Đại lượng A
và B được gọi là các tham số của hàm hiệu chuẩn đường thẳng Y = A +
BX. A và B
còn được dùng để ký hiệu các biến (giả) trong biểu thức liên quan đến các tham
số hàm hiệu chuẩn.
4.3 Đại lượng Xi và Yi được dùng
làm biến (giả) để ký hiệu cho tọa độ của điểm dữ liệu thứ i.
4.4 Các hằng số A*
và B* là giá trị
(chưa biết) của A và B xác định hàm hiệu chuẩn đường thẳng Y =
A* + B*X đối với hệ thống đo cụ thể đang xét.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.6 xi và yi
là giá trị đo được của tọa độ của điểm dữ liệu thứ i.
4.7 a và b
là các ước lượng của tham số hàm hiệu chuẩn đối với hệ thống đo.
4.8 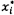 và
và 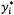 là các ước lượng của tọa độ của điểm dữ liệu thứ
i thỏa mãn
là các ước lượng của tọa độ của điểm dữ liệu thứ
i thỏa mãn 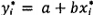 .
.
4.9 Véc tơ kích
thước m x 1 được ký
hiệu là:

và ma trận kích thước m x n được ký hiệu
là:

Kích thước của véc tơ hoặc ma trận
luôn được quy định để tránh nhầm lẫn
có thể có.
4.10 T ký
hiệu cho chuyển vị.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.12 Một số ký hiệu
có nhiều hơn một nghĩa. Bối cảnh sẽ làm rõ việc sử dụng.
4.13 Các số trình
bày trong các bảng tới số chữ số thập phân xác định là các đại diện được làm
tròn chính xác của
các số lưu giữ ở độ chụm cao hơn, ví dụ như trong trường hợp bảng tính. Do đó, có thể nhận thấy sự
không thống nhất nhỏ giữa tổng cột hiển thị và tổng cột các số hiển thị.
4.14 Trong một số
bảng, số điều nhỏ ở trên một cột hoặc các cột chỉ ra nơi mà công thức được cho
để xác định các giá trị bên dưới.
4.15 Trong các ví
dụ, trong khi giá trị dữ liệu được cung cấp với độ chụm đã cho thì các kết quả
tính toán được cung cấp với độ chụm cao hơn để cho phép người sử dụng so sánh kết
quả khi thực hiện tính toán.
5 Các nguyên tắc hiệu
chuẩn đường thẳng
5.1 Khái
quát
5.1.1 Điều này xem
xét hệ thức Y = A + BX mô tả biến
phụ thuộc Y (còn gọi là
‘đáp ứng’) như hàm của biến độc lập X (còn gọi là ‘mô phỏng’) có thể được xác
định từ dữ liệu đo như thế nào. Trong bối cảnh hiệu chuẩn, dữ liệu đo phát sinh
khi phương tiện đo được quy định bởi các giá trị A* và B* (chưa biết)
của tham số hàm hiệu chuẩn được ‘mô phỏng’ bằng vật mẫu với giá trị hiệu chuẩn của Xi được cho
theo đơn vị của chuẩn, của tính chất của vật mẫu, và ‘đáp ứng’
tương ứng hoặc số chỉ Yi của phương
tiện được ghi lại. Hệ thức này cung cấp đáp ứng Y của hệ
thống dựa vào vật mẫu có đại lượng được hiệu chuẩn X. Quá trình này được
gọi là ‘đánh giá tiếp’. Hữu ích hơn trong thực tiễn là hệ thức này cho phép
chuyển đổi đáp ứng đo được y của Y thành ước lượng
x, theo các
đơn vị của chuẩn, của tính chất X của vật mẫu. Quá trình này được gọi là ‘đánh
giá ngược’ hoặc ‘dự đoán’.
5.1.2 Việc hiệu chuẩn
hệ thống đo cần tính đến độ không đảm bảo đo, và, nếu có, hiệp phương sai gắn với
dữ liệu đo. Đầu ra của quy trình hiệu chuẩn là hàm hiệu chuẩn được sử dụng cho
dự đoán (và, nếu cần, đánh giá tiếp). Đầu ra cũng bao gồm độ không đảm bảo chuẩn và hiệp
phương sai gắn với ước lượng a và b của tham
số mô tả hàm hiệu chuẩn, được sử dụng để đánh giá độ không đảm bảo chuẩn gắn với
dự đoán (và đánh giá tiếp).
5.2 Đầu vào
để xác định hàm hiệu chuẩn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Thông tin yêu cầu để xác định hàm hiệu
chuẩn đường thẳng là dữ liệu đo và độ không đảm bảo chuẩn kèm theo cùng với hiệp
phương sai. Trong tiêu chuẩn này, dữ liệu đo được ký hiệu bằng (xi, yi), i = 1,…, m, tức là m cặp giá trị đại lượng đo được của X và Y.
Giả định rằng m ít nhất bằng hai và các giá trị của xi không bằng
nhau.
CHÚ THÍCH: Độ không đảm bảo kèm theo
các ước lượng a và b thường giảm khi m tăng. Do đó, hiệu
chuẩn cần hướng tới sử dụng càng nhiều điểm dữ liệu đo được nếu khả thi về kinh tế.
5.2.2 Độ không đảm
bảo kèm theo và hiệp phương sai
Độ không đảm bảo chuẩn gắn với xi và yi được ký hiệu
tương ứng là u(xi) và u(yi).
Hiệp phương sai gắn với xi và xj được ký hiệu
là cov(xi, xj). Tương tự,
giá trị gắn với yi và yj và với xi và yj được ký hiệu
tương ứng là cov(yi, yj) và cov(xi, yi).
Phụ lục D chỉ ra cách độ không đảm bảo và hiệp phương sai gắn với biến đáp ứng và
biến mô phỏng đo được có thể được đánh giá và đưa ra giải thích về thông tin độ
không đảm bảo đó. Thông tin
hoàn chỉnh về độ không đảm bảo được trình bày bằng dãy các phần tử (ma trận) U
kích thước 2m x 2m chứa các phương sai (độ không đảm bảo chuẩn
bình phương) u2(xi) và u2(yi) và các hiệp
phương sai:

Đối với nhiều ứng dụng, một số hoặc tất
cả các hiệp phương sai được lấy bằng 0 (xem 5.3).
CHÚ THÍCH: Tiêu chuẩn này liên quan đến
các vấn đề trong đó u(xi) hoặc u(yi) thường khác
nhau.
5.3 Xác định
hàm hiệu chuẩn
5.3.1 Đầu vào để
xác định hàm hiệu chuẩn là dữ liệu đo, độ không đảm bảo kèm theo và các hiệp
phương sai có thể có. Cho trước các tham số A và B, đầu vào có thể
sử dụng để cung cấp thước đo sai lệch của điểm dữ liệu thứ i (xi,
yi) so với đường
thẳng Y= A + BX. Các ước lượng
a và b được xác định bằng cách tối thiểu hóa tổng bình
phương các sai lệch này, hoặc thước đo chung hơn khi mọi hiệp phương sai khác
0. Điều này đạt được như thế nào tùy thuộc vào ‘cấu trúc độ không đảm bảo’ gắn
với dữ liệu đo. Cấu trúc này
liên quan đến câu trả lời cho các câu hỏi sau đây:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
ii) Hiệp phương sai gắn với cặp giá trị
đo được là không đáng kể?
5.3.2 Trong tiêu
chuẩn này xem xét các trường hợp sau đây, được cho theo thứ tự phức tạp tăng dần
và tùy thuộc vào câu trả lời cho các câu hỏi ở 5.3.1:
a) Chỉ có độ không đảm bảo gắn với giá
trị đo được
yi và tất cả
các hiệp phương sai gắn với dữ liệu được coi là không đáng kể (Điều 6);
b) Độ không đảm bảo gắn với giá trị đo
được xi và yi và tất cả
các hiệp phương sai gắn với dữ liệu được coi là không đáng kể (Điều 7);
c) Độ không đảm bảo gắn với giá trị đo được xi và yi và chỉ các
hiệp phương sai gắn với cặp (xi, yi) (Điều 8);
d) Chỉ có độ không đảm
bảo gắn với giá trị đo được yi và chỉ các hiệp
phương sai gắn với yi và yj (i ≠ j) (Điều 9);
e) Trường hợp chung nhất trong đó có độ
không đảm bảo gắn với giá trị đo được xi và yi và hiệp
phương sai gắn với tất cả các cặp giá trị của xi, xj, và yi
(Điều 10).
5.3.3 Đối với từng
trường hợp trong 5.3.2 được cho
a) dữ liệu đo và cấu trúc độ không đảm
bảo quy định,
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
c) vấn đề bình phương tối thiểu nhắm đến,
d) các bước tính toán,
e) tính chất của mô hình thống kê,
f) giá trị sử dụng của mô hình,
g) tổ chức tính toán cho máy tính, khi
thích hợp,
h) thuật toán số, khi thích hợp, và
i) một hoặc nhiều ví dụ thực tế.
5.4 Xử lý số
Phụ lục C đưa ra cách tiếp cận
chung cho trường hợp tổng quát nhất là e) trong 5.3.2. Nó có thể sử dụng để xử
lý tất cả các trường hợp khác và sử dụng các phương pháp tinh vi, ổn định về số
học. Tuy nhiên, các trường hợp từ a) đến c) trong 5.3.2 có thể được xử lý bằng
cách sử dụng các thao tác cơ bản, ví dụ, có thể thực hiện trong bảng tính. Các
trường hợp d) và e) trong 5.3.2 đòi hỏi một số thao tác ma trận, dễ áp dụng
theo ngôn ngữ máy tính hỗ trợ số học ma trận, nhưng không phù hợp lắm cho tính bằng bảng
tính.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.5.1 Đối với tất cả
các trường hợp xem xét, các ước lượng của tham số hàm hiệu chuẩn có thể được thể
hiện (rõ ràng hoặc hàm ý) như hàm của dữ liệu đo. Các nguyên tắc của GUM [TCVN
9595-3:2013 (ISO/IEC Guide 98-3:2008)] có thể được áp dụng để lan truyền độ
không đảm bảo và hiệp phương sai gắn với dữ liệu đo thông qua các hàm này để
thu được giá trị gắn với các ước lượng tham số này. Theo cách này, dữ liệu đo
được sử dụng để cung cấp ước
lượng a và b của tham số hàm hiệu chuẩn, và để đánh giá độ không
đảm bảo chuẩn u(a) và u(b)
và hiệp phương sai cov(a,b) gắn với các ước lượng này. Đối với
trường hợp a) và d) trong 5.3.2, sự lan truyền là chính xác vì ước lượng tham số
có thể được biểu thị như tổ hợp tuyến tính của các đầu vào yi. Đối với các
trường hợp khác, trong đó ước lượng tham số không thể biểu thị như vậy thì lan truyền
là gần đúng, dựa trên tuyến tính hóa về ước lượng tham số. Vì nhiều mục đích,
giá trị gần đúng thu được bằng phép tuyến tính hóa sẽ đủ chính xác.
CHÚ THÍCH: Khi lan truyền độ không đảm
bảo là gần đúng, và đặc biệt nếu độ không đảm bảo liên quan lớn (ví dụ, trong một
số lĩnh vực đo sinh học), thì có thể sử dụng cách tiếp cận dựa trên lan truyền
phân bố. Cách tiếp cận này [ISO/IEC Guide 98-3:2008/Suppl. 1:2008] sử dụng phương
pháp Monte Carlo (không đề cập trong tiêu chuẩn này).
5.5.2 Các đầu ra
chính trong mô tả hàm hiệu chuẩn đường thẳng là véc to ước lượng
tham số a kích thước 2 x 1 và ma trận hiệp phương sai Ua kích thước 2 x 2 được cho bởi

trong đó u(a) và u(b)
là độ không đảm bảo chuẩn gắn với a và b, tương ứng, và cov(a,b) = cov(b,a) là hiệp
phương sai gắn với a và b.
5.6 Xác nhận
giá trị sử dụng của mô hình
5.6.1 Trong việc
xác định ước lượng a và b của tham số hàm hiệu chuẩn đường thẳng,
giả định rằng mô hình Y = A + BX là hợp lý và độ
không đảm bảo gắn với dữ liệu đo đưa ra thước đo tin cậy về độ lệch của dữ liệu
đo so với đường thẳng. Khi a và b đã được xác định, độ lệch thực
tế của điểm dữ liệu so với hàm hiệu chuẩn khớp tốt nhất có thể được đánh giá dựa
trên độ lệch dự đoán. So sánh này liên quan đến thước đo tổng hợp độ lệch biểu
thị bằng tổng các bình
phương 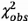 của m
phần dư có trọng số, phần dư có trọng số thứ i là thước đo độ lệch của điểm dữ liệu
thứ i so với đường
thẳng, hoặc, khi hiệp phương sai gắn với điểm dữ liệu thứ i (xi, yi) là khác 0
so với một dạng tổng quát hơn. Nếu
của m
phần dư có trọng số, phần dư có trọng số thứ i là thước đo độ lệch của điểm dữ liệu
thứ i so với đường
thẳng, hoặc, khi hiệp phương sai gắn với điểm dữ liệu thứ i (xi, yi) là khác 0
so với một dạng tổng quát hơn. Nếu 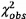 lớn hơn nhiều so với dự kiến thì trên cơ sở
thống kê, có lý do để đặt ra câu hỏi về hiệu lực của các giả định mô hình.
lớn hơn nhiều so với dự kiến thì trên cơ sở
thống kê, có lý do để đặt ra câu hỏi về hiệu lực của các giả định mô hình.
5.6.2 Từ quan điểm
thống kê, dữ liệu đo có thể được coi như các thể hiện của biến ngẫu nhiên. Nếu
đã biết phân bố xác suất đặc trưng cho các biến ngẫu nhiên này thì về nguyên tắc
có thể xác định phân bố xác suất cho thước đo tổng hợp độ lệch trong 5.6.1. Khi
đó, xác suất có thể được tính là
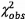 , coi như được lấy từ
phân bố tổng hợp này, vượt quá phân vị cụ thể bất kỳ của phân bố. Tuy nhiên, vì
thông tin về các đại lượng này thường giới hạn ở bản thân các giá trị đo được
và phương sai kèm theo (lấy là kỳ vọng và phương sai, tương ứng, của biến ngẫu
nhiên đặc trưng bởi các phân bố
này), nên không có đủ thông tin để xác định phân bố cho thước đo này. Thay vào
đó, việc đánh giá hiệu lực được thực hiện với giả định rằng phân bố của các đại
lượng là phân bố chuẩn. Với giả định này, duy trì từ giờ về sau, ít nhất là cho
mục đích xác nhận giá trị sử dụng, phân bố cho thước đo này là
, coi như được lấy từ
phân bố tổng hợp này, vượt quá phân vị cụ thể bất kỳ của phân bố. Tuy nhiên, vì
thông tin về các đại lượng này thường giới hạn ở bản thân các giá trị đo được
và phương sai kèm theo (lấy là kỳ vọng và phương sai, tương ứng, của biến ngẫu
nhiên đặc trưng bởi các phân bố
này), nên không có đủ thông tin để xác định phân bố cho thước đo này. Thay vào
đó, việc đánh giá hiệu lực được thực hiện với giả định rằng phân bố của các đại
lượng là phân bố chuẩn. Với giả định này, duy trì từ giờ về sau, ít nhất là cho
mục đích xác nhận giá trị sử dụng, phân bố cho thước đo này là 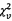 với n = m - 2 bậc tự do.
Theo đó, xác suất mà
với n = m - 2 bậc tự do.
Theo đó, xác suất mà 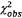 vượt
quá phân vị cụ thể bất kỳ của
vượt
quá phân vị cụ thể bất kỳ của 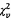 có thể được xác định (xem 6.3, 7.3, 9.3 và
10.3). Sử dụng phân vị 95 %.
có thể được xác định (xem 6.3, 7.3, 9.3 và
10.3). Sử dụng phân vị 95 %.
CHÚ THÍCH 1: Nếu 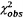 vượt quá phân vị 95 % của
vượt quá phân vị 95 % của 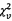 thì hàm hiệu chuẩn
đường thẳng có thể được coi như không giải thích cho dữ liệu đủ tốt vì mục đích thực
tế. Trong trường hợp này, dữ liệu và độ không đảm bảo kèm theo cần được kiểm
tra về khả năng sai lỗi. Hàm hiệu chuẩn bao gồm đa thức của X có bậc 2
hoặc cao hơn hoặc một dạng toán học khác có thể được bàn đến; xem xét như vậy nằm
ngoài phạm vi
tiêu chuẩn này.
thì hàm hiệu chuẩn
đường thẳng có thể được coi như không giải thích cho dữ liệu đủ tốt vì mục đích thực
tế. Trong trường hợp này, dữ liệu và độ không đảm bảo kèm theo cần được kiểm
tra về khả năng sai lỗi. Hàm hiệu chuẩn bao gồm đa thức của X có bậc 2
hoặc cao hơn hoặc một dạng toán học khác có thể được bàn đến; xem xét như vậy nằm
ngoài phạm vi
tiêu chuẩn này.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.6.3 Để thu được
càng nhiều giá trị càng tốt từ hàm hiệu chuẩn, mong muốn là độ không đảm bảo đầu
vào cần được rút ra trước khi xác định tham số hàm hiệu chuẩn chứ không phải được
đánh giá khi khớp với dữ liệu đã được xác định, với độ không đảm bảo kèm theo ước
lượng từ dữ liệu hoặc biết theo hệ số thang đo. Trường hợp đề cập sau được xem
xét trong Phụ lục E.
5.6.4 Nếu trong trường
hợp cụ thể bất kỳ, việc xác nhận giá trị của mô hình không đạt, tức là 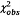 vượt quá phân vị 95 % của
vượt quá phân vị 95 % của
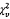 (xem 5.6.2), thì độ
không đảm bảo chuẩn u(a) và u(b), hiệp phương sai
cov(a,b) tính được
(xem 5.5.2) cần được coi là không đáng tin cậy, khi độ không đảm bảo gắn với
giá trị dự đoán (xem 5.7).
(xem 5.6.2), thì độ
không đảm bảo chuẩn u(a) và u(b), hiệp phương sai
cov(a,b) tính được
(xem 5.5.2) cần được coi là không đáng tin cậy, khi độ không đảm bảo gắn với
giá trị dự đoán (xem 5.7).
5.7 Sử dụng
hàm hiệu chuẩn
5.7.1 Hàm hiệu chuẩn
thường được sử dụng cho việc dự đoán (đánh giá ngược) trong đó, dựa vào ước lượng
của Y và độ không đảm bảo chuẩn kèm theo, giá trị tương ứng của X
được ước lượng và độ không đảm bảo chuẩn kèm theo được đánh giá. Việc
đánh giá độ không đảm bảo đề cập sau sử dụng độ không đảm bảo chuẩn gắn với các ước
lượng a và b cũng như hiệp phương sai kèm theo của chúng. Xem
11.1.
5.7.2 Đôi khi cần
có đánh giá tiếp trong đó giá trị
tương ứng của Y thu được cùng với độ không đảm bảo chuẩn kèm theo, dựa
vào ước lượng của X và độ không đảm bảo kèm theo, ví dụ, khi so sánh các
hiệu chuẩn của một tập hợp các phương tiện đo tương tự nhau. Xem 11.2.
CHÚ THÍCH: Giả định rằng điều kiện đo
duy trì trong quá
trình hiệu chuẩn giữ nguyên ở thời điểm hàm hiệu chuẩn được sử dụng về sau. Nếu không, sẽ cần
một hiệu chuẩn mới hoặc thực hiện việc điều chỉnh thích hợp để tính
đến thay đổi bất kỳ như độ trôi có thể xảy ra (và độ không đảm bảo kèm theo bất
kỳ cũng được xử lý). Biểu đồ
kiểm soát có thể
hữu ích cho mục đích này.
5.8 Xác định
đường thẳng bình phương tối thiểu thông thường khớp nhất với dữ liệu
5.8.1 Đường thẳng
bình phương tối thiểu thông thường (không trọng số) khớp nhất với dữ liệu được
xác định bằng các giá trị a và b của tham số A và B
tối thiểu hóa

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Các giá trị này thỏa mãn công thức đã
cho bằng cách cho đạo hàm riêng bậc một của biểu thức (2) đối với A và B
bằng 0.
5.8.2 Có thể tính a
và b theo các bước sau đây:

5.8.3 Giá trị x0 và y0 sao cho đường
khớp nhất với các điểm dữ liệu chuyển đổi 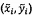 đi qua gốc và có cùng độ dốc như với đường
khớp nhất với các điểm dữ liệu gốc (xi, yi).
đi qua gốc và có cùng độ dốc như với đường
khớp nhất với các điểm dữ liệu gốc (xi, yi).
CHÚ THÍCH: Về mặt toán học, các tham số khớp nhất được
xác định bằng cách giải cặp phương trình tuyến tính liên quan đến ma
trận kích thước 2
x 2. Đối với
các điểm dữ liệu chuyển đổi, ma trận
này là đường chéo, cho phép dễ dàng xác định các tham số nghiêm. Chuyển đổi dữ liệu
cũng có tác dụng hữu ích về độ chính xác số học của giải pháp tính toán [4,
trang 33].
5.8.4 Các phương
pháp mô tả trong Điều 6 đến Điều 10 dưới đây tạo thành phần mở rộng của các các tính
toán trong 5.8.2 có tính đến
thông tin về độ không đảm bảo quy định.
6 Mô hình dùng cho độ
không đảm bảo gắn với yi
6.1 Khái
quát
6.1.1 Điều này xem
xét trường hợp 5.3.2 a), tức là khi thông tin dưới đây được cung cấp cho i = 1,..., m:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
b) độ không đảm bảo chuẩn u(yi) gắn với yi.
Phụ lục D cung cấp hướng dẫn về việc
thu được các độ không đảm bảo này. Tất cả các độ không đảm bảo và hiệp phương
sai khác gắn với dữ liệu được coi là không đáng kể.
6.1.2 Trường hợp
5.3.2 a) tương ứng với mô tả bởi mô hình thống kê
yi
= A* + B*xi + ei1
i = 1,..., m,
(3)
trong đó ei là thể hiện của các
biến ngẫu nhiên độc lập với kỳ vọng 0 và phương sai u2(yi)
[9, trang 1]. A* và B* là các giá trị (chưa biết) của tham số hàm
hiệu chuẩn cho hệ thống đo yêu cầu hiệu chuẩn và cung cấp dữ liệu đo. Mô hình
này được gọi là mô hình hàm, không có độ không đảm bảo gắn với xi.
6.1.3 Lấy wi
= 1/u(yi), i = 1,..., m.
Các ước lượng a và b là giá trị tối thiểu hóa tổng các bình phương có trọng
số

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
đối với A và B. Vấn đề tối
thiểu hóa này được gọi là vấn đề bình phương tối thiểu có trọng số (WLS). Các ước
lượng này thỏa mãn công thức đã cho bằng cách gắn các đạo hàm riêng bậc
một của biểu thức (4) đối với A và B bằng 0.
6.2 Các ước
lượng tham số hiệu chuẩn, độ không đảm bảo chuẩn và hiệp phương sai kèm theo
6.2.1 Các ước lượng
a và b được tính ở các bước từ 1 đến 5; độ không đảm bảo chuẩn u(a) và u(b) còn hiệp
phương sai cov(a, b) được đánh
giá ở bước 6:

CHÚ THÍCH 1: Các bước 1 đến 5 tương ứng với các
bước:

CHÚ THÍCH 2: Các bước từ 1 đến 5 xác định
phép tính bình phương tối
thiểu cho hệ thống các công thức
wia + wixib = wiyi, i =
1,..., m.
CHÚ THÍCH 3: Nếu u(yi) giống nhau,
sao cho wi giống nhau, thì a
và b giống với giá trị cho bởi đường bình phương tối thiểu thông thường khớp
nhất trong 5.8.2.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
6.2.2 Các ước lượng
a và b xác định trong 6.1.3 có các tính chất sau
đây [15] đối với dữ liệu yi theo mô hình (3):
i) Các ước lượng a và b được cho bởi
tổ hợp tuyến tính các dữ liệu yi.
ii) Các ước lượng a và b
được coi là các thể hiện của biến ngẫu nhiên có kỳ vọng tương ứng là A* và B*.
iii) Ma trận hiệp phương sai đối với
biến ngẫu nhiên trong ii) được quy định là u2(a), u2(b)
và cov(a,b) tính được trong 6.2.1.
Tính chất i) nêu rõ a và b được rút ra
bằng cách sử dụng phương pháp ước lượng tuyến tính. Tính chất ii) nêu rõ rằng
phương pháp ước lượng tuyến tính là không chệch. Tính chất ii) và iii) cùng cho
thấy rằng phương pháp ước lượng là nhất quán theo nghĩa khi số lượng m điểm dữ
liệu tăng lên, thì ước lượng a và b hội tụ A* và B*,
tương ứng.
Phương pháp ước lượng của 6.1.3 có tính chất tối
ưu sau đây đối với dữ liệu yi theo mô hình (3):
iv) Các ước lượng 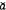 và
và 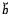 cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ có thể được coi là các thể hiện của biến ngẫu
nhiên có phương sai ít nhất là lớn bằng phương sai gắn với phương pháp ước lượng WLS.
cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ có thể được coi là các thể hiện của biến ngẫu
nhiên có phương sai ít nhất là lớn bằng phương sai gắn với phương pháp ước lượng WLS.
Tính chất iv) có thể được giải thích
như dưới đây. Đối với hằng số c và d, độ không đảm bảo chuẩn 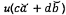 gắn với tổ hợp tuyến tính
các ước lượng
gắn với tổ hợp tuyến tính
các ước lượng 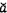 và
và  cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ ít nhất là lớn bằng u(ca + db). Các
tính chất từ i) đến iv) chứng tỏ việc sử dụng phương pháp bình phương tối thiểu
cho dữ liệu tương thích với mô hình (3). Lưu ý là khi sử dụng mô hình này, các
tuyên bố chỉ được đưa ra về kỳ vọng và phương sai gắn với ei; các phân bố
kèm theo không được quy định thêm. Nếu đưa ra giả định bổ sung rằng ei là thể hiện
của biến ngẫu nhiên phân bố chuẩn thì khi đó các tính chất khác gắn với phương
pháp ước lượng WLS có thể đưa ra:
cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ ít nhất là lớn bằng u(ca + db). Các
tính chất từ i) đến iv) chứng tỏ việc sử dụng phương pháp bình phương tối thiểu
cho dữ liệu tương thích với mô hình (3). Lưu ý là khi sử dụng mô hình này, các
tuyên bố chỉ được đưa ra về kỳ vọng và phương sai gắn với ei; các phân bố
kèm theo không được quy định thêm. Nếu đưa ra giả định bổ sung rằng ei là thể hiện
của biến ngẫu nhiên phân bố chuẩn thì khi đó các tính chất khác gắn với phương
pháp ước lượng WLS có thể đưa ra:
v) Các biến ngẫu nhiên trong ii) được
đặc trưng bởi phân bố chuẩn hai chiều tập trung ở A* và B* với ma
trận hiệp phương sai quy định bởi u2(a), u2(b) và cov(a,b).
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
vii) Trong bối cảnh suy luận
Bayes, phân bố trong phạm vi kiến thức cho A và B, đã cho dữ liệu
đo quan trắc yi, là phân bố chuẩn hai chiều tập trung ở a và b với ma trận hiệp phương sai xác định bởi u2(a)
và u2(b) và cov(a,b).
6.3 Xác nhận
giá trị sử dụng của mô hình
Nếu m > 2 thì giá trị sử dụng của mô
hình có thể kiểm nghiệm một phần bằng cách sử dụng phần dư có trọng số ri (tiếp theo
6.2.1):
7 Thiết lập ri = wi(yi
– a – bxi),
i
= 1,..., m;
8 Thiết lập giá
trị Khi-bình phương quan trắc 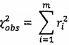 và bậc tự do n = m - 2;
và bậc tự do n = m - 2;
9 Kiểm tra xem
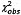 có vượt quá
phân vị 95 % của
có vượt quá
phân vị 95 % của 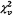 không,
và xem liệu có bác bỏ mô hình đường
thẳng hay không.
không,
và xem liệu có bác bỏ mô hình đường
thẳng hay không.
CHÚ THÍCH: Kiểm nghiệm
Khi-bình phương dựa
trên giả định là ei trong mô hình (3) là
các thể hiện của biến
ngẫu nhiên chuẩn độc lập.
6.4 Tổ chức
các tính toán
Các tính toán trong 6.2.1 và 6.3 có thể
được tổ chức thành một hoặc hai bảng để thực hiện trong bảng tính như trong Bảng
2 và Bảng 3, có thể hợp nhất thành một bảng hoặc bảng tính.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

Bảng 3 - Tổ
chức tính toán để xác định hàm hiệu chuẩn đường thẳng bằng bình phương tối thiểu
có trọng số

VÍ DỤ: (TRỌNG SỐ BẰNG NHAU) Bằng 4 đưa ra
sáu điểm dữ liệu và độ không đảm bảo chuẩn kèm theo. Giá trị đo được xi được lấy là
chính xác và độ không đảm bảo chuẩn gắn với giá trị đo được yi là u(yi) = 0,5. Do đó,
trọng số được lấy là wi = 1/u(yi) = 2,0, i = 1...., 6.
Bảng 4- Dữ liệu
thể hiện sáu điểm đo, trọng số bằng nhau
xi
yi
u(yi)
1,0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,5
2,0
5,6
0,5
3,0
7,1
0,5
4,0
9,3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5,0
10,7
0,5
6,0
12,1
0,5
Tham số đường thẳng khớp nhất được
tính như trong Bảng 5. Từ bảng này, go = 84,000/24,000 =
3,500, h0 =
192,400/24,000 = 8,017, b = 123,000/70,000 = 1,757 và a = 8,017 - (1,757)(3,500)
= 1,867.
Bảng 5 - Bảng
tính toán gắn với dữ liệu trong Bảng 4
wi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66


gi
hi

gihi
ri

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.500
8.017
a = 1.867
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.000
13.200
-5.000
-9.433
25.000
47.167
-0.648
0.419
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
8.000
22.400
-3.000
-4.833
9.000
14.500
0.438
0.192
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
12.000
28.400
-1.000
-1.833
1.000
1.833
-0.076
0.006
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
10.000
37.200
1.000
2.567
1.000
2.567
0.810
0.655
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
20.000
42.800
3.000
5.367
9.000
16.100
0.095
0.009
2.000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
24.000
48.400
5.000
8.167
25.000
40.833
-0.619
0.383
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
84.000
192.400
70.000
123.000
b = 1,757
1.665
Độ không đảm bảo chuẩn và hiệp phương
sai gắn với tham số được làm khớp cũng có thể được đánh giá, sử dụng công thức
trong 6.2.1, từ thông tin trong Bảng 5:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
u2(b) = 1/70,000,
như vậy u(b) = 0,120;
u(a, b) = -3,500/70,000 =
-0,050.
Giá trị Khi-bình phương quan trắc được
là 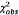 = 1,665 với n = 4 bậc tự do, như
tính được ở Bảng 5 sử dụng 6.3. Vì
= 1,665 với n = 4 bậc tự do, như
tính được ở Bảng 5 sử dụng 6.3. Vì 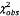 không vượt quá phân vị 95 % của
không vượt quá phân vị 95 % của 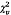 , tức là 9,488, nên không
có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
, tức là 9,488, nên không
có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
Dữ liệu và hàm hiệu chuẩn đường thẳng
khớp được trình bày trên Hình 2. Độ không đảm bảo chuẩn gắn với yi
được minh họa (và trong các hình tiếp sau) bằng đường thẳng đứng, tập trung vào
yi và có các cực trị yi - u(yi) và yi
+ u(yi). Phần dư có trọng số được trình
bày trên Hình 3.

Hình 2 - Dữ
liệu trong Bảng 4 và hàm hiệu chuẩn đường thẳng khớp thu được trong Bảng 5

Hình 3 - Phần
dư có trọng số ri thu được
trong Bảng 5
VÍ DỤ: (TRỌNG SỐ KHÔNG BẰNG NHAU)
Bảng 6 đưa ra sáu điểm dữ liệu và độ
không đảm bảo chuẩn kèm theo. Giá trị đo được xi được lấy là
chính xác. yi thu được bằng cách sử dụng hai thiết lập
phương tiện, sao cho giá trị X càng lớn thì yi càng kém
chính xác.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
xi
yi
u(yi)
1,0
3,2
0,5
2,0
4,3
0,5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7,6
0,5
4,0
8,6
1,0
5,0
11,7
1,0
6,0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1,0
Tham số đường thẳng khớp nhất được
tính như trong Bảng 7. Từ bảng này, g0 =
39,000/15,000 = 2,600, h0 = 93,500/15,000 =
6,233, b = 65,000/31,600 = 2,057 và a = 6,233 - (2,057)(2,600) =
0,885.
Bảng 7 - Bảng
tính toán gắn với dữ liệu trong Bảng 6
w2



gi
hi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
gihi
ri

2.600
6.233
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
a = 0.885
2.000
4.000
4.000
12.800
-3.200
-0,007
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
10.413
0.510
0.200
2.000
4.000
8.000
17.200
-1.200
-3.867
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.040
-1.398
1.955
2.000
4.000
12.000
30.400
0.800
0.733
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.187
1.088
1.183
1.000
1.000
4.000
8.600
1.400
2.367
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.313
-0.513
0.263
1.000
1.000
5.000
11.700
2.400
5.467
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
13.120
0.830
0.281
1.000
1.000
6.000
12.800
3.400
6.567
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
22.327
-0.427
0.182
15.000
39.000
93.500
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
63.000
b = 2.057
4.131
Độ không đảm bảo chuẩn
và hiệp phương sai gắn với tham số được làm khớp cũng có thể được đánh giá, sử
dụng công thức trong 6.2.1, từ thông tin trong Bảng 7:
u2(a) = 1/15,000
+(2,600)2/31,600, như vậy u(a) = 0,530;
u2(b) = 1/31,600,
như vậy u(b) = 0,178;
u(a, b) =
-2,600/31,600 = -0,082.
Giá trị Khi-bình phương quan trắc được
là 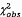 = 4,131 với v = 4 bậc tự
do, như tính được ở Bảng 7 sử dụng 6.3. Vì
= 4,131 với v = 4 bậc tự
do, như tính được ở Bảng 7 sử dụng 6.3. Vì 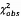 không vượt quá phân vị 95 % của
không vượt quá phân vị 95 % của 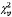 tức là 9,488, nên không
có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
tức là 9,488, nên không
có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
Dữ liệu và hàm hiệu chuẩn đường thẳng
khớp được trình bày trên Hình 4. Phần dư có trọng số được trình bày trên Hình 5.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình 4 - Dữ
liệu trong Bảng 6 và hàm hiệu chuẩn đường thẳng khớp thu được trong Bảng 7

Hình 5 - Phần dư có trọng
số ri thu được
trong Bảng 7
7 Mô hình độ không đảm
bảo gắn với xi và yi
7.1 Khái
quát
7.1.1 Điều này xem
xét trường hợp 5.3.2 b), tức là khi thông tin dưới đây được cung cấp cho i = 1,…, m:
a) dữ liệu đo (xi, yi),
b) độ không đảm bảo chuẩn u(xi)
gắn với xi, và
b) độ không đảm bảo chuẩn u(yi) gắn với yi.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7.1.2 Trường hợp
5.3.2 b) tương ứng với mô tả bởi mô hình thống kê

trong đó di và ei là thể hiện
của các biến ngẫu nhiên độc lập với kỳ vọng 0 và phương sai tương ứng là u2(xi) và u2(yi).
Mô hình này được gọi là mô hình hàm số. Trong mô hình, (xi, yi) đại diện cho
tọa độ đo được của điểm (không quan trắc được) 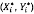 nằm trên đường
nằm trên đường 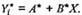 .
.
7.1.3 Vì xi (cùng với yi - xem Điều
6) có độ không đảm bảo kèm theo nên cũng phải tính đến chúng khi xác định hàm
hiệu chuẩn đường thẳng. Vấn đề
xác định a và b trong bối cảnh này là một trong hồi quy khoảng
cách trực giao có trọng số (ODR có trọng số) hoặc hồi quy khoảng cách tổng quát
hóa (GDR) [2]. Trong tài liệu thống kê nó được gọi là mô hình sai số-trong-biến
[7], [9, trang 50], [17, trang 189], Các ước lượng a và b là ước
lượng tối thiểu hóa tổng các bình
phương

(6)
đối với A, B và Xi,
i = 1,..., m,
các trọng số ni = 1/u(xi) và wi
= 1/u(yi). Mỗi ước lượng
giải
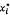 , cùng với a
và b, xác định ước lượng
, cùng với a
và b, xác định ước lượng 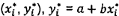 , của
, của 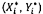 trong mô hình (5).
trong mô hình (5).
7.1.4 Cho trước A và B,
các giá trị 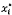 tối thiểu
hóa tổng các bình phương (6) đối với Xi được cho bởi
tối thiểu
hóa tổng các bình phương (6) đối với Xi được cho bởi

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Sử dụng biểu thức (7) vấn đề tối ưu
hóa có thể được đặt ra đối với tham số A và B độc lập bằng cách
thay thế Xi trong biểu thức (6) bằng 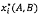 , có
, có

7.1.5 Nếu

thì tổng các bình phương (8) tương đương với

Số hạng Ri có giải thích
hình học dưới đây. Véc tơ vuông góc với đường thẳng Y = A + BX được cho bởi
(-B,1)T/(1
+ B2)1/2 và Ri là bội số trọng
số của thành phần có dấu của 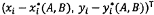 theo chiều của véc tơ vuông góc.
theo chiều của véc tơ vuông góc.
CHÚ THÍCH 1: Bình phương tối
thiểu thông thường (xem 5.8) và bình phương tối thiểu có trọng số (xem Điều 6),
khoảng cách tới đường thẳng được đo ‘theo chiều thẳng đứng’, tức là, theo chiều Y, phản ánh thực
tế là độ lệch của điểm đo được (xi, yi) so với đường
thẳng có thể được tính về số hạng sai số ei kèm theo yi, vì xi được giả định
là đã biết chính xác. ODR có trọng số giải quyết trường hợp trong đó còn có độ
không đảm bảo gắn với xi.
CHÚ THÍCH 2: Biểu thức (7) được cho bằng
cách cho đạo hàm riêng bậc một của biểu thức (6) đối với A, B và Xi
bằng 0.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 4: Nếu u(xi) = u(yi) = ui thì khi đó 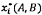 xác định điểm trên đường
thẳng Y= A + BX gần nhất với (xi, yi) và
xác định điểm trên đường
thẳng Y= A + BX gần nhất với (xi, yi) và
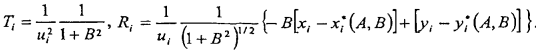
Vì véc tơ vuông góc với đường thẳng là
(-B,1)T/(1
+ B2)1/2, nên Ri là khoảng cách
có trọng số tính từ điểm (xi, yi) tới đường
thẳng Y= A + BX.
7.1.6 Điều 7.1.3
liên quan đến A, B và Xi,
i
=
1,..., m, như các biến trong tối thiểu hóa. Các tính toán nêu trong 7.2.1 thực
hiện quá trình tối thiểu hóa này trong phép lặp hai giai đoạn [2]:
i) từ các gần đúng với a và b,
xác định tối ưu 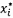 tương
ứng, và
tương
ứng, và
ii) đối với các 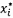 này, xác định các gần đúng mới với
a và b sẽ làm giảm tổng các bình phương (6).
này, xác định các gần đúng mới với
a và b sẽ làm giảm tổng các bình phương (6).
CHÚ THÍCH: Không có phân biệt nào về
ký hiệu giữa 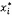 ở phép lặp điển
hình và giá trị
tính được cuối cùng.
ở phép lặp điển
hình và giá trị
tính được cuối cùng.
7.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
7.2.1 Các ước lượng
a và b được tính ở các bước từ 1 đến 6 dưới đây sử dụng quy trình
lặp chỉ ra ở 7.1.6; độ không đảm bảo chuẩn u(a), u(b) và hiệp
phương sai cov(a,b) được đánh
giá ở bước 7 (xem Phụ lục B):
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

4 Xác định giải
pháp bình phương tối
thiểu (không có trọng số) δa và δb cho hệ thức

đó là

5 Cập nhật các
xấp xỉ hiện tại cho các tham số và phần dư: 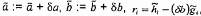 , i = 1,..., m
, i = 1,..., m
6 Lặp lại các
bước từ 2 đến 5 cho đến khi đạt được sự hội tụ. Đặt 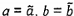 ;
;
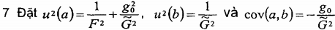 ;
;
trong đó g0, h0, ...là các giá
trị tính được ở
bước
4.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 2: Ở bước 2, 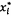 xác định điểm
xác định điểm 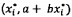 trên xấp xỉ hiện tại với
hàm hiệu chuẩn đường thẳng khớp nhất là gần nhất, như khoảng cách có trọng số,
với điểm dữ liệu đo được (xi, yi).
trên xấp xỉ hiện tại với
hàm hiệu chuẩn đường thẳng khớp nhất là gần nhất, như khoảng cách có trọng số,
với điểm dữ liệu đo được (xi, yi).
CHÚ THÍCH 3: Ở bước 3, hi
tính được đại
diện cho giá trị của khoảng cách tổng quát hóa Ri trong biểu
thức (9) từ điểm dữ liệu thứ i đến ước lượng hiện tại của hàm hiệu
chuẩn đường thẳng. Thuật toán được thiết kế để tối thiểu hóa tổng
các bình phương của các khoảng cách này.
CHÚ THÍCH 4: Ở bước
4, các hiệu chỉnh δa và δb thường
sẽ giảm độ lớn bằng hệ số hằng số gần đúng giữa các phép lặp. Mức độ giảm phụ
thuộc chủ yếu vào độ không đảm bảo gắn với dữ liệu: độ không đảm bảo càng nhỏ thì mức giảm sẽ
càng nhiều. Quy trình lặp có thể
kết thúc khi độ lớn của các hiệu chỉnh được điều chỉnh đến mức không đáng
kể.
CHÚ THÍCH 5: Phần dư tính được ở bước 5 được gắn
với phép giải hệ thức tính ở bước 4. Tại
điềm hội tụ, ri tính được ở bước 5 bằng hi
tính được ở bước 3.
CHÚ THÍCH 6: Hoàn toàn chỉ yêu cầu các
phần dư tính được ở bước 5 trong
lần lặp cuối. Tuy nhiên, để dễ trình bày dạng bảng (Bảng 9 ở 7.4), phần
dư được tính tại mỗi lần
lặp.
CHÚ THÍCH 7: u2(a), u2(b) và cov(a,b)
trong bước 7 thu được bằng cách áp dụng định luật lan truyền độ không đảm bảo
trong TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008) cho a và b như
được cung cấp bởi các bước 1 đến 6.
7.2.2 Trong khi có
thể rút ra các tính chất trong 6.2.2 đối với phương pháp ước lượng WLS thì thực
tế là các ước lượng a và b xác định bằng
cách tối thiểu hóa tổng các bình phương (6) phụ thuộc phi tuyến vào dữ liệu xi và yi nghĩa là
không thể dễ dàng nêu rõ các tính chất tương ứng đối với ODR có trọng số. Các ước
lượng a và b xác định trong 7.1.3 có các tính chất sau đây đối với dữ liệu
xi và yi theo mô hình
(5):
i) Các ước lượng a và b
được cho bởi hàm phi tuyến của các dữ liệu xi và yi.
ii) Các ước lượng a và b
được coi là các thể hiện của biến ngẫu nhiên có kỳ vọng tương ứng là A*
và B* gần đúng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Các gần đúng trong ii) và iii) sẽ chính
xác hơn đối với dữ liệu có độ không đảm bảo kèm theo nhỏ hơn. Tuy nhiên, phương
pháp ước lượng có tính chất nhất quán sau đây:
iv) Đối với dữ liệu thỏa mãn mô hình
(5), khi số lượng m điểm dữ liệu tăng, các ước lượng a và b hội tụ
đến A* và B*, tương ứng [16].
Ngược lại, phương pháp ước lượng WLS
thường sẽ ước lượng thấp độ lớn của tham số độ dốc [5] đối với dữ liệu tạo ra
theo mô hình (5).
Nếu giả định bổ sung được đưa ra là di
và ei là các thể
hiện của biến ngẫu nhiên phân bố chuẩn thì các tính chất khác gắn với
phương pháp ước lượng ODR có trọng số có thể được nêu ra:
v) Các biến ngẫu nhiên trong ii) được
đặc trưng gần đúng bởi phân bố chuẩn hai chiều tập trung ở A* và B*
với ma trận hiệp phương sai quy định bởi u2(a), u2(b) và cov(a,b).
vi) Các ước lượng a và b là ước
lượng hợp lý lớn nhất,
tương ứng với giá trị hợp lý nhất của A và B có thể làm tăng dữ
liệu đo quan trắc được xi và yi.
vii) Trong bối cảnh suy luận Bayes,
phân bố trong phạm vi kiến thức cho A và B, đã cho dữ liệu đo
quan trắc xi và yi, là xấp xỉ
phân bố chuẩn hai chiều tập trung ở a
và b với ma trận hiệp phương sai xác định bởi u2(a), u2(b)
và cov(a,b).
7.3 Xác nhận
giá trị sử dụng của mô hình
Nếu m > 2 thì giá trị sử dụng
của mô hình có thể kiểm nghiệm một phần bằng cách sử dụng phần dư ri có trọng số
tính được trong bước 5 ở 7.2.1 ở lần lặp cuối cùng, tức là sự hội tụ (tiếp tục
từ 7.2.1):
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
9 Kiểm tra xem 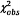 có vượt quá phân vị 95 %
của
có vượt quá phân vị 95 %
của 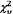 không, và xem liệu
có bác bỏ mô hình đường thẳng hay không.
không, và xem liệu
có bác bỏ mô hình đường thẳng hay không.
CHÚ THÍCH: Kiểm nghiệm
Khi-bình phương dựa trên giả định là di và ei trong mô hình (5) là các thể hiện của biến
ngẫu nhiên chuẩn độc lập và phép gần đúng bậc một.
7.4 Tổ chức
tính toán
Các tính toán trong 7.2.1 và 7.3 có thể
được tổ chức thành hai bảng liên tiếp, phù hợp để thực hiện trong bảng tính. Bảng
thứ nhất (Bảng 8), đưa ra các xấp xỉ 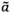 và
và 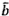 (xem 7.2.1 bước 1), tính fi, gi
và hi (xem 7.2.1 bước 3). Bảng thứ hai (Bảng 9) sử dụng
các giá trị
fi,
gi
và hi này để tính các hiệu chính δa và δb (xem 7.2.1 bước 4).
(xem 7.2.1 bước 1), tính fi, gi
và hi (xem 7.2.1 bước 3). Bảng thứ hai (Bảng 9) sử dụng
các giá trị
fi,
gi
và hi này để tính các hiệu chính δa và δb (xem 7.2.1 bước 4).
Bảng 8 - Tính
toán để xác định hàm hiệu chuẩn đường thẳng, đã cho các xấp xỉ 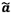 và
và 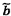 với các ước lượng tham số đường thẳng
a và b
với các ước lượng tham số đường thẳng
a và b

Bảng 9 - Tổ chức tính
toán để xác định các hiệu chính δa và δb cho hàm hiệu chuẩn đường
thẳng GDR

VÍ DỤ: Bảng 10 đưa ra sáu điểm dữ liệu
đo được và độ không đảm bảo chuẩn kèm theo.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
xi
w(xi)
yi
u(yi)
1,2
0,2
3,4
0,2
1,9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4,4
0,2
2,9
0,2
7,2
0,4
4,0
0,2
8,5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4,7
0,2
10,8
0,4
5,9
0,2
13,5
0,4
Để xác định các xấp xỉ 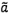 và
và 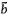 ban đầu (7.2.1 bước 1), hàm hiệu chuẩn đường
thẳng bình phương tối thiểu có trọng số được xác định. Tiếp theo quy trình mô tả
trong 6.2, thu được các dữ liệu cho trong Bảng 11 và Bảng 12.
ban đầu (7.2.1 bước 1), hàm hiệu chuẩn đường
thẳng bình phương tối thiểu có trọng số được xác định. Tiếp theo quy trình mô tả
trong 6.2, thu được các dữ liệu cho trong Bảng 11 và Bảng 12.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
xi
yi
u(yi)
1,2
3,4
0,2
1,9
4,4
0,2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7,2
0,4
4,0
8,5
0,4
4,7
10,8
0,4
5,9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,4
Bảng 12 - Bảng
tính toán gắn với dữ liệu trong Bảng 11 để xác định các xấp xỉ 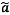 và
và 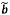 ban đầu
ban đầu
wi



gi
hi

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
ri

2.573 3
6.186 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.000 0
25.000 0
30.000 0
65.000 0
-6.866 7
-13.933 3
47.151 1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.818 6
0.670 1
5.000 0
25.000 0
47.500 0
110.000 0
-3.366 7
-8.933 3
11.334 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-1.700 6
2.892 0
5.000 0
25.000 0
72.500 0
180.000 0
1.633 3
5.066 7
2.667 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.557 7
2.426 4
2.500 0
6.250 0
25.000 0
53.125 0
3.566 7
5.783 3
12.721 1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-1.879 1
3.531 0
2.500 0
6.250 0
29.375 0
67.500 0
5.316 7
11.533 3
28.266 9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.111 3
0.012 4
2.500 0
6.250 0
36.875 0
84.375 0
8.316 7
18.283 3
63.166 9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.416 3
0.173 3
93.750 0
241.250 0
580.000 0
171.308 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
b = 2.148 3
9.705 2
Các xấp xỉ ban đầu là 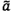 = 0,658 3 và
= 0,658 3 và 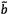 = 2,148 3. Với các xấp
xỉ này, bảng dữ liệu đầu tiên (Bảng 13) có dạng trong Bảng 8 có thể được tính để
thu được
fi, gi và hi. Bảng dữ liệu
thứ hai (Bảng 14) có dạng trong Bảng 9 khi đó tính các số gia δa = -0,078 4 và δb = 0,011 1
(7.2.1 bước 4). Ở cuối phép lặp, các xấp xỉ
= 2,148 3. Với các xấp
xỉ này, bảng dữ liệu đầu tiên (Bảng 13) có dạng trong Bảng 8 có thể được tính để
thu được
fi, gi và hi. Bảng dữ liệu
thứ hai (Bảng 14) có dạng trong Bảng 9 khi đó tính các số gia δa = -0,078 4 và δb = 0,011 1
(7.2.1 bước 4). Ở cuối phép lặp, các xấp xỉ 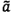 và
và 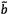 được cập nhật (7.2.1 bước 5):
được cập nhật (7.2.1 bước 5):

Với các giá trị 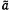 và
và 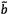 cập nhật này, hai dữ liệu bảng mới được hình
thành (Bảng 15 và Bảng 16) đề xác định thêm các hiệu chính δa = = -0,001
0 và δb = 0,000 2.
Quá trình này được lặp lại lần thứ ba (Bảng 17 và Bảng 18). Trong trường hợp
này, độ lớn của các hiệu chính nhỏ hơn 0,000 05, được điều chỉnh để thành không
đáng kể cho mục đích này, và các xấp xỉ cuối cùng cho ước lượng tham số là a
= 0,578 8 và b = 2,159 7.
cập nhật này, hai dữ liệu bảng mới được hình
thành (Bảng 15 và Bảng 16) đề xác định thêm các hiệu chính δa = = -0,001
0 và δb = 0,000 2.
Quá trình này được lặp lại lần thứ ba (Bảng 17 và Bảng 18). Trong trường hợp
này, độ lớn của các hiệu chính nhỏ hơn 0,000 05, được điều chỉnh để thành không
đáng kể cho mục đích này, và các xấp xỉ cuối cùng cho ước lượng tham số là a
= 0,578 8 và b = 2,159 7.
Độ không đảm bảo chuẩn và hiệp phương
sai (7.2.1 bước 7) gắn với tham số được làm khớp cũng có thể được đánh giá từ
thông tin trong bảng cuối cùng (Bảng 18):

Giá trị Khi-bình phương quan trắc được
là 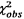 = 2,743 với n = 4 bậc tự do, như
tính được ở Bảng 18 sử dụng
7.3. Vì
= 2,743 với n = 4 bậc tự do, như
tính được ở Bảng 18 sử dụng
7.3. Vì 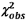 không vượt
quá phân vị 95 % của
không vượt
quá phân vị 95 % của 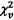 ,
tức là 9,488, nên
không có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
,
tức là 9,488, nên
không có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và dữ liệu.
Các điểm dữ liệu và hàm hiệu chuẩn đường
thẳng ODR có trọng số được trình bày bằng đồ thị trên Hình 6. Đối với mỗi giá
trị i, đồ thị cũng đưa ra vị trí của 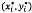 , điểm trên đường thẳng gần nhất về mặt xác
suất với điểm dữ liệu (xi,yi). Phần dư có
trọng số được minh họa trên Hình 7.
, điểm trên đường thẳng gần nhất về mặt xác
suất với điểm dữ liệu (xi,yi). Phần dư có
trọng số được minh họa trên Hình 7.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
xi
u(xi)
yi
u(yi)
ti

zi
fi
gi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.658 3
2.148 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.200 0
0.200 0
3.400 0
0.200 0
4.452 2
1.262 6
0,163 7
2.110 0
2.664 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.900 0
0.200 0
4.400 0
0.200 0
4.452 2
1.769 9
-0.340 1
2.110 0
3.734 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.900 0
0.200 0
7.200 0
0.200 0
4.452 2
3.019 2
0.311 6
2.110 0
6.370 6
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.000 0
0.200 0
8.500 0
0.400 0
2.901 9
3.812 6
-0.751 5
1.703 5
6.494 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.700 0
0.200 0
10.800 0
0,400 0
2.901 9
4.711 1
0.044 7
1.703 5
8.025 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.900 0
0.200 0
13.000 0
0.400 0
2.901 9
5.941 6
0.166 7
1.703 5
10.121 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Bảng 14 - Lần
lặp đầu tiên để xác định các hiệu chính δa và δb, cho trước fi, gi và hi

figi
fihi




ri
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.123 9
-0.043 7
δa = -0.078 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.621 6
0.729 0
-3.927 3
0.437 8
15.423 0
-1.719 3
0.481 4
0.231 8
4.452 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-1.514 1
-2.857 0
-0.625 3
8.162 3
1.786 4
-0.593 5
0.352 3
4.452 2
13.442 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.220 9
0.749 8
0.048 8
0.165 6
0.752 3
0.565 9
2.901 9
11.063 6
-2.180 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-1.205 7
1.376 4
-1.414 5
-1.218 7
1.485 2
2.901 9
13.671 0
0.129 7
2.703 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7.310 8
0.407 3
0.120 6
0.014 5
2.901 9
17.241 6
0.483 5
4.799 9
0.358 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.720 6
0.305 2
0.093 1
22.062 2
68.919 9
-0.964 8
55.360 6
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
δb = 0.011 1
2.742 9
Bảng 15 - Như
Bảng 13 nhưng cho lần lặp thứ hai
xi
u(xi)
yi
u(yi)
ti

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
fi
gi
hi
0.579 9
2.159 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.200 0
0.200 0
3.400 0
0.200 0
4.414 6
1.287 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.101 1
2.704 7
0.480 8
1.900 0
0.200 0
4.400 0
0.200 0
4.414 6
1.792 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.101 1
3.705 5
-0.594 1
2.900 0
0.200 0
7.200 0
0.200 0
4.414 6
3.030 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.101 1
6.379 9
0.751 9
4.000 0
0.200 0
8.500 0
0.400 0
2.885 8
3.821 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.698 8
6.491 3
-1.218 9
4.700 0
0.200 0
10.800 0
0.400 0
2.885 8
4.717 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.698 8
8.014 2
0.120 5
5.900 0
0.200 0
13.500 0
0.400 0
2.885 8
5.944 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.698 8
10.098 8
0.305 1
Bảng 16 - Như
Bảng 14 nhưng cho lần lặp thứ hai

figi
fihi


...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

ri

3.141 2
-0.000 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
δa = -0.001 0
4.414 6
5.682 7
1.010 3
-3.895 3
0.481 4
15.173 4
-1.875 1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.232 6
4.414 6
7.911 7
-1.248 2
-2.834 4
-0.593 5
8.033 9
1.682 2
-0.592 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.414 6
13.404 7
1.579 8
-0.220 1
0.752 4
0.048 4
-0.165 6
0.752 5
0.566 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
11.027 1
-2.070 6
1.155 1
-1.218 4
1.334 2
-1.407 4
-1.218 7
1.485 2
2.885 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.204 6
2.678 1
0.120 9
7.172 0
0.323 8
0.120 3
0.014 5
2.885 8
17.155 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.762 6
0.305 6
22.682 4
1.455 3
0.304 4
0.092 7
21.901 2
68.790 1
-0.005 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
54.444 3
0.013 2
δb = 0.000 2
2.742 7
Bảng 17 - Như
Bảng 13 nhưng cho lần lặp thứ ba
xi
u(xi)
yi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
ti

zi
fi
gi
hi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.578 8
2.159 7
1.200 0
0.200 0
3.400 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.413 8
1.287 5
0.229 6
2.100 9
2.705 0
0.482 3
1.900 0
0.200 0
4.400 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.413 8
1.792 4
-0.282 2
2.100 9
3.765 7
-0.592 8
2.900 0
0.200 0
7.200 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.413 8
3.036 6
0.358 2
2.100 9
6.379 5
0.752 5
4.000 0
0.200 0
8.500 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.885 5
3.821 2
-0.717 4
1.698 7
6.490 9
-1.218 7
4.700 0
0.200 0
10.800 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.885 5
4.717 6
0.070 8
1.698 7
8.013 7
0.120 3
5.900 0
0.200 0
13.500 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.885 5
5.944 7
0.179 2
1.698 7
10.098 0
0.304 4
Bảng 18 - Như
Bảng 14 nhưng cho lần lặp thứ ba

figi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66




ri

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
δa = 0.000 0
4.413 8
5.682 9
1.013 3
-3.894 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
15.168 5
-1.878 5
0.482 8
0.232 7
4.413 8
7.911 3
1.245 4
-2.834 0
-0.592 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.680 0
-0.592 8
0.351 4
4.413 8
13.402 7
1.580 9
-0.220 2
0.752 5
0.048 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.752 5
0.566 2
2.885 5
11.025 8
-2.070 2
1.154 8
-1.218 7
1.333 5
-1.407 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.485 2
2.885 5
13.612 6
0.204 3
2.677 6
0.120 3
7.169 5
0.322 0
0.120 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2.885 5
17.153 1
0.517 1
4.761 9
0.304 4
22.675 6
1.449 6
0.304 4
0.092 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
68.788 4
0.000 0
54.427 1
0.000 1
δb = 0.000 0
2.742 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Hình 6 - Dữ
liệu trong Bảng 10 và hàm hiệu chuẩn đường thẳng khớp thu được trong Bảng 11 đến
18

Hình 7 - Khoảng
cách có trọng số thu được trong Bảng 18
8 Mô hình độ không đảm
bảo gắn với xi và yi và hiệp phương sai gắn với cặp (xi, yi)
8.1 Khái
quát
8.1.1 Điều này xem
xét trường hợp 5.3.2 c), tức là khi thông tin sau đây được cung cấp cho i = 1,…, m:
a) dữ liệu đo (xi, yi),
b) độ không đảm bảo chuẩn u(xi) gắn với xi,
c) độ không đảm bảo chuẩn u(yi) gắn với yi, và
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ lục D cung cấp hướng dẫn về việc
thu được các độ không đảm bảo và hiệp phương sai này. Tất cả các hiệp phương
sai khác gắn với dữ liệu được coi là không đáng kể.
8.1.2 Trường hợp
5.3.2 c) tương ứng với mô tả bởi mô hình thống kê

trong đó mỗi cặp (di,ei) là thể hiện
của các biến ngẫu nhiên hai chiều với kỳ vọng (0,0)T và ma trận hiệp
phương sai có thành phần đường chéo u2(xi) và u2(yi) và thành phần
ngoài đường chéo cov (xi, yi) = cov(yi,xi), tức là

độc lập với các biến ngẫu nhiên khác.
CHÚ THÍCH: Giả định rằng (di,ei) là các thể hiện của biến
ngẫu nhiên chuẩn hai chiều chỉ cần thiết cho việc xác nhận giá trị sử dụng của
mô hình (10).
8.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
8.2.1 Về thuật toán,
trường hợp này có thể được xử lý bằng cách mở rộng (xem Phụ lục B) xử lý trong
Điều 7. Các tính toán giống hệt như trong Điều 7, ngoại trừ bước 2 trong 7.2.1
được thay bằng
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
8.2.2 Tất cả các
tính chất nêu trong 7.2.2 áp dụng cho dữ liệu được tạo ra theo mô hình (10) và
tuân thủ theo phần còn lại của Điều 7.
9 Mô hình độ không đảm
bảo và hiệp phương sai gắn với yi
9.1 Khái
quát
9.1.1 Điều này xem
xét trường hợp 5.3.2 d), tức là khi thông tin sau đây được cung cấp cho i
= 1,..., m:
a) dữ liệu đo (xi,
yi),
b) độ không đảm bảo chuẩn u(yi) gắn với yi, và
c) hiệp phương sai cov(yi, yj) gắn với cặp
(yi, yj) j =
1,... ,
m, j ≠ i.
9.1.2 Độ không đảm
bảo chuẩn bình phương và hiệp phương sai bao gồm ma trận hiệp phương sai

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
9.1.3 Trường hợp
5.3.2 d) tương ứng với mô tả bởi mô hình thống kê

(11)
trong đó e = (e1,..., em)T là thể hiện
của biến ngẫu nhiên đa biến với kỳ vọng véc tơ bằng véc tơ 0 có kích thước m
x 1 và ma trận hiệp phương sai có kích thước m x m bằng
Uy [21].
9.1.4 Các ước lượng
a và b là giá trị tối thiểu hóa tổng các bình phương tổng
quát [8]

trong đó e = y - A1 - Bx, đối với A
và B. Vấn đề xác định a và b trong bối cảnh này được gọi
là một trong hồi quy Gauss-Markov (GMR) [2].
CHÚ THÍCH: Đối với trường hợp trong đó
Uy là đường chéo, tổng bình phương tổng quát hóa
(12) đơn giản thành biểu thức (4) trong 6.1.3 dẫn đến vấn đề WLS.
9.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
9.2.2 Ước lượng tham
số a và b được tính ở các bước từ 1 đến 7 dưới đây; độ không đảm
bảo chuẩn u(a) và u(b) và hiệp phương sai cov(a,b) được đánh
giá trong bước 8:
1 Tính thừa số
Cholesky Ly kích thước m x m của Uy
= LyLyT; xem A.4.1;
2 Lấy 1 là véc
tơ của một có kích thước m x 1. Giải ba hệ thức tam giác dưới Lyf = 1, Lyg
= x và Lyh = y, trong đó f = (f1,..., fm)T,... đối với f, g và h; xem A.4.3;

9.2.3 Ước lượng a và b xác định
trong 9.1.4 có các tính chất sau đây [15] đối với dữ liệu yi
theo mô hình (11):
i) Các ước lượng a và b được cho
bởi tổ hợp tuyến tính các dữ liệu yi.
ii) Các ước lượng a và b
được coi là các thể hiện của biến ngẫu nhiên có kỳ vọng tương ứng là A*
và B*.
iii) Ma trận hiệp phương sai đối với
biến ngẫu nhiên trong ii) được quy định là u2(a), u2(b) và cov(a,b) tính được
trong 9.2.2.
Tính chất i) nêu rõ a và b được rút ra
bằng cách sử dụng phương pháp ước lượng tuyến tính. Tính chất ii) nêu rõ rằng
phương pháp ước lượng tuyến tính là không chệch. Tính chất ii) và iii)
cùng cho thấy rằng phương pháp ước lượng là nhất quán theo nghĩa khi số lượng m
điểm dữ liệu tăng lên, thì ước lượng a và b hội tụ A* và B*,
tương ứng.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
iv) Các ước lượng 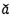 và
và 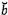 cung cấp bởi phương pháp ước lượng tuyến tính không chệch
bất kỳ có thể được coi là các thể hiện của biến ngẫu nhiên có phương sai ít nhất
là lớn bằng phương sai gắn với phương pháp ước lượng GMR.
cung cấp bởi phương pháp ước lượng tuyến tính không chệch
bất kỳ có thể được coi là các thể hiện của biến ngẫu nhiên có phương sai ít nhất
là lớn bằng phương sai gắn với phương pháp ước lượng GMR.
Tính chất iv) có thể được giải thích như dưới
đây. Đối với hằng số c và d, độ không đảm bảo chuẩn 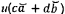 gắn với tổ hợp tuyến tính các ước
lượng
gắn với tổ hợp tuyến tính các ước
lượng 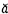 và
và 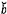 cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ ít nhất là lớn bằng u(ca + db). Các tính chất
từ i) đến iv) chứng tỏ việc sử dụng phương pháp bình phương tối thiểu cho dữ liệu tương
thích với mô hình (11).
Lưu ý là khi sử dụng mô hình
này, các tuyên bố chỉ được đưa ra về kỳ vọng và phương sai gắn với ei; các phân bố
kèm theo không được quy định thêm. Nếu đưa ra giả định bổ sung rằng ei là thể hiện
của biến ngẫu nhiên đặc trưng bởi phân bố chuẩn nhiều chiều thì khi đó các tính
chất khác gắn với phương pháp ước lượng GMR có thể đưa ra:
cung cấp bởi phương pháp ước
lượng tuyến tính không chệch bất kỳ ít nhất là lớn bằng u(ca + db). Các tính chất
từ i) đến iv) chứng tỏ việc sử dụng phương pháp bình phương tối thiểu cho dữ liệu tương
thích với mô hình (11).
Lưu ý là khi sử dụng mô hình
này, các tuyên bố chỉ được đưa ra về kỳ vọng và phương sai gắn với ei; các phân bố
kèm theo không được quy định thêm. Nếu đưa ra giả định bổ sung rằng ei là thể hiện
của biến ngẫu nhiên đặc trưng bởi phân bố chuẩn nhiều chiều thì khi đó các tính
chất khác gắn với phương pháp ước lượng GMR có thể đưa ra:
v) Các biến ngẫu nhiên trong ii) được
đặc trưng bởi phân bố chuẩn hai
chiều tập trung ở A* và B* với ma trận
hiệp phương sai quy định bởi u2(a), u2(b) và cov(a,b).
vi) Các ước lượng a và b
là ước lượng hợp lý lớn nhất, tương ứng với giá trị hợp lý nhất của A và
B có thể làm tăng dữ liệu đo quan trắc được yi.
vii) Trong bối cảnh suy luận Bayes,
phân bố trong phạm vi kiến thức cho A và B, đã cho dữ liệu đo
quan trắc
yi, là phân bố
chuẩn hai chiều tập trung ở a và b với ma trận hiệp
phương sai xác định bởi u2(a), u2(b) và cov(a,b).
CHÚ THÍCH 1: Các tính chất liệt
kê ở trên giống với
trong phương pháp ước lượng WLS của 6.1.3 đối với dữ liệu tạo ra theo mô hình (3).
CHÚ THÍCH 2: u2(a), u2(b) và cov(a,b)
trong bước 8 thu được bằng cách áp dụng định luật lan truyền độ không đảm bảo trong
TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008) cho a và b như cung cấp
bởi các bước từ 1 đến 7.
9.3 Xác nhận
giá trị sử dụng của mô hình
Nếu m > 2 thì giá trị sử dụng
của mô hình có thể kiểm nghiệm một phần bằng cách sử dụng phần dư ri
có trọng số (tiếp theo 9.2.2):
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
10 Thiết lập
giá trị Khi-bình phương quan trắc được 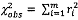 và bậc tự do n = m - 2;
và bậc tự do n = m - 2;
11 Kiểm tra xem 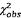 có vượt quá phân vị 95 %
của
có vượt quá phân vị 95 %
của 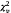 không, và xem liệu
có bác bỏ mô hình đường thẳng hay không.
không, và xem liệu
có bác bỏ mô hình đường thẳng hay không.
CHÚ THÍCH: Kiểm nghiệm Khi-bình phương dựa
trên giả định là ei trong mô hình (11)
là các thể hiện của biến ngẫu nhiên chuẩn độc lập đặc trưng bởi phân bố chuẩn
nhiều chiều.
9.4 Tổ chức
tính toán
Các tính toán trong 9.2.2 và 9.3 có thể
được tổ chức thành các bảng như trong các bảng từ 19 đến 21. Bảng 20 chứa fi,
gi và hi tính được ở bước 1 và 2 trong 9.2.2 đối
với thừa số hóa Cholesky Ly của ma trận hiệp phương sai Uy.
Bảng 21 sử dụng các fi, gi và hi
này để tính các ước lượng a và b của tham số hàm hiệu chuẩn đường thẳng.
Bảng 19 - Dữ
liệu cho hàm hiệu chuẩn đường thẳng Gauss-Markov

Bảng 20 -
Tính toán ban đầu để xác định
hàm hiệu chuẩn đường thẳng Gauss-Markov

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

VÍ DỤ: Bảng 22 đưa ra mười điểm dữ liệu
đo được (xi, yi) và độ không
đảm bảo chuẩn gắn với yi.
Dữ liệu thu được bằng cách sử dụng mô
hình mô tả trong D.2.2 với uR = 1,0, uS,1 = 1,0 và uS,2 = 2,0.
Bảng 22 - Dữ
liệu thể hiện mười điểm đo, yi có ma trận
hiệp phương sai kèm
theo
xi
yi
1,0
1,3
2,0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3,0
6,9
4,0
7,5
5,0
10,2
6,0
12,0
7,0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
8,0
17,1
9,0
19,5
10,0
21,0
Ma trận hiệp phương sai Uy
kích thước 10
x 10 gắn với yi là

Thừa số Cholesky Ly
kích thước 10
x 10 của Uy
= LyLyT, tính được sử dụng một
trong hai thuật toán mô tả trong A.4.1, là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Các véc tơ f, g và h trong Bảng
23 được tính theo bước 2 trong 9.2.2.
Bảng 23 -
Tính toán ban đầu bảng kèm theo dữ liệu trong Bảng 22
fi
gi
hi
0,707 1 0,408 2 0,288 7 0,223 6 0,182 6 0,447 2 0,149 1 0,092 5 0,067
3 0,052 9
0,707 1 1,224 7 1,732 1 2,236 1 2,738 6 2,683 3 1,639 8 1,849 0 2,219 8 2,646 3
0,919 2 2,816 9 4,416 7 3,957 8 5,696 3 5,366 6 3,652 2 4,428
4 5,320 8 5,536 0
Tham số đường thẳng khớp nhất trong Bảng
24 được tính theo Bảng 21. Từ Bảng 24, g0 = 4,404 8/1,071
4 = 4,111 1, h0 = 9,0048/1,071 4 = 8,404 4, b =
54,218 5/24,629 6 = 2,201 4 và a = 8,404 4 – (2,201
4)(4,111 1) = -0,645 6.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

figi
fihi




ri

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.111 1
8.404 4
a = -0,645 6
0.500 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.650 0
-2.199 9
-5.023 6
4.839 5
11.051 4
-0.180 9
0.032 7
0.166 7
0.500 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-0.453 6
-0.614 2
0.205 8
0.278 6
0.394 4
0.147 7
0.083 3
0.500 0
1.275 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.990 6
0.297 3
1.085 4
0.790 2
0.624 5
0.050 0
0.500 0
0.885 0
1.316 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.734 0
2.737 0
-0.820 2
0.672 7
0.033 3
0.500 0
1.040 0
1.988 0
4.161 9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
8.273 9
-0.214 5
0.046 0
0.200 0
1.2000
2.400 0
0.844 7
1.608 0
0.713 6
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-0.251 6
0.063 3
0.022 2
0.244 4
0.544 4
1.020 9
2.399 4
1.054 6
2.464 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.019 2
0.008 5
0.170 9
0.409 4
1.468 9
3.651 4
2.457 8
5.363 6
0.417 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0,004 5
0.149 3
0.357 9
1.943 3
4.755 5
3.776 3
9.241 2
0.477 7
0.228 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.140 1
0.293 0
2.428 7
5.091 2
5.898 6
12.365 0
-0.255 2
0.065 1
1.071 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
9.004 8
24.629 6
54.218 5
b = 2.201 4
2.074 0
Các độ không đảm bảo chuẩn và hiệp
phương sai gắn với a và b được đánh giá từ Bảng 24 sử dụng bước 8
trong 9.2.2:

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Các điểm dữ liệu và hàm hiệu chuẩn đường
thẳng khớp như trình bày trên Hình 8. Phần dư có trọng số được minh họa trên
Hình 9.

Hình 8 - Dữ
liệu trong Bảng 22 và hàm hiệu chuẩn đường thẳng khớp thu được trong Bảng 24

Hình 9 - Phần
dư có trọng số ri tính được
trong Bảng 24
10 Mô hình độ không
đảm bảo và hiệp phương sai gắn với xi và yi
10.1 Khái
quát
10.1.1 Điều này xem
xét trường hợp 5.3.2 e), tức là trường hợp chung nhất trong đó tất cả các dữ liệu
đo đều kèm theo độ không đảm bảo và hiệp phương sai. Phụ lục D cung cấp hướng dẫn
để thu được các độ không đảm bảo và hiệp phương sai này.
10.1.2 Độ không đảm
bảo chuẩn và hiệp phương sai bao gồm ma trận hiệp phương sai
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
kích thước 2m x 2m gắn với
véc tơ (x1,..., xm,
y1,..., ym)T của dữ liệu
đo kích thước 2m x 1.
10.1.3 Trường hợp
5.3.2 e) tương ứng với mô tả bởi mô hình thống kê
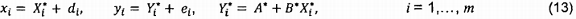 trong đó véc tơ (d1,…, dm, e1,..., em)T kích thước 2m
x 1 là thể hiện của biến ngẫu nhiên đa biến với kỳ vọng véc tơ bằng véc tơ 0 có kích thước 2m
x 1 và ma trận hiệp phương sai có kích thước 2m x 2m bằng U [21].
trong đó véc tơ (d1,…, dm, e1,..., em)T kích thước 2m
x 1 là thể hiện của biến ngẫu nhiên đa biến với kỳ vọng véc tơ bằng véc tơ 0 có kích thước 2m
x 1 và ma trận hiệp phương sai có kích thước 2m x 2m bằng U [21].
10.1.4 Các ước lượng
a và b là giá trị tối
thiểu hóa tổng các bình phương tổng quát

trong đó d = x - X và e = y - A1 - Bx, đối với A, B và Xi, i = 1,..., m. Vấn đề xác định a và b trong bối cảnh này được gọi
là một trong hồi quy Gauss-Markov tổng quát hóa (GGMR) [2].
10.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
10.2.1 Nếu U hoàn toàn
dương, thì tồn tại thừa số Cholesky L tam giác dưới kích thước 2m
x 2m của U = LLT [10] (xem
thêm A.4), ước lượng a và b của A và B có thể được
tính theo quy trình lặp sử dụng thao tác ma trận-véc tơ. Nếu không có thể cần đến
nhiều phương pháp số học hơn. Các thao tác này chuyển đổi tổng bình phương tổng quát hóa (14) thành
tổng bình phương thông thường (2) như trong 5.8.1, tức là, vấn đề trở thành
bình phương tối thiểu không trọng số và không có hiệp phương sai. Quy trình lặp
cũng liên quan đến các xấp xỉ 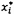 , xác định các điểm
, xác định các điểm 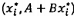 trên đường gần nhất với điểm dữ liệu đo được
(xi, yi), trong đó độ gần được
đo theo khoảng cách có trọng số, có tính đến thông tin về độ không đảm bảo xác
định bởi U.
trên đường gần nhất với điểm dữ liệu đo được
(xi, yi), trong đó độ gần được
đo theo khoảng cách có trọng số, có tính đến thông tin về độ không đảm bảo xác
định bởi U.
10.2.2 Ước lượng a
và b được tính ở các bước từ
1 đến 10 dưới đây sử dụng quy trình lặp như nêu trong 6.2.1; độ không đảm bảo
chuẩn u(a) và u(b) và hiệp phương sai cov(a,b) được đánh
giá trong bước 11:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
2 Tính véc tơ
kích thước 2m x 1,

và ma trận (Jacobi) kích thước 2m
x (m + 2).

trong đó 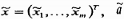 và
và 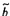 được trích từ ước lượng
được trích từ ước lượng 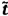 hiện tại của véc tơ tham số;
hiện tại của véc tơ tham số;
3 Tính thừa số
Cholesky L kích thước 2m x 2m của U
= LLT [10]; xem
A.4.1;
4 Giải hệ tam
giác dưới

để xác định véc tơ chuyển đổi 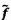 kích thước 2m x 1 và ma trận
chuyển đổi
kích thước 2m x 1 và ma trận
chuyển đổi 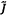 kích thước 2m x (m + 2); xem
A.4.3;
kích thước 2m x (m + 2); xem
A.4.3;
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
6 Xác định thừa
số Cholesky M, ma trận tam giác dưới kích thước (m + 2) x (m
+ 2) trong 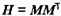 ; xem
A.4.1;
; xem
A.4.1;
7 Giải hệ tam
giác dưới Mq = -g để xác định véc tơ q kích thước (m
+ 2) x 1 ; xem A.4.3;
8 Giải hệ tam
tác trên 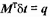 để xác định
véc tơ hiệu chính δt kích thước (m
+ 2) x 1; xem A.4.4;
để xác định
véc tơ hiệu chính δt kích thước (m
+ 2) x 1; xem A.4.4;
9 Cập nhật các
xấp xỉ hiện tại cho các tham số: 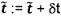 ;
;
10 Lặp lại các
bước từ 2 đến 9 cho đến khi đạt được sự hội tụ. Đặt 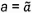 và
và 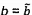 (các thành phần m + 1 và m + 2 của
(các thành phần m + 1 và m + 2 của 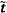 );
);
11 Phân vùng M
thu được trong bước 6 là

trong đó

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

CHÚ THÍCH 1: Trong bước 1, các xấp xỉ ban đầu được
cung cấp bởi 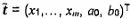 , trong
đó a0 và b0 là giá trị
tham số đường thẳng xác định bởi
bình phương tối thiểu có trọng số khớp với dữ liệu; xem 6.2.1.
, trong
đó a0 và b0 là giá trị
tham số đường thẳng xác định bởi
bình phương tối thiểu có trọng số khớp với dữ liệu; xem 6.2.1.
CHÚ THÍCH 2: Trong bước 8, véc tơ hiệu
chính δt thường sẽ giảm
về độ lớn bằng hệ số hằng số gần đúng giữa các phép lặp. Mức độ giảm phụ thuộc
chủ yếu vào độ không đảm bảo gắn với dữ liệu: độ không đảm bảo càng nhỏ thì mức
giảm sẽ càng nhiều. Quy trình lặp có thể kết thúc khi độ lớn của các hiệu chỉnh được điều
chỉnh đến mức
không đáng kể.
CHÚ THÍCH 3: Trong bước 8, hiệu chính δt được cho bởi
phép giải bình phương tối
thiểu của công thức ma trận

cách giải được xác định bởi công thức
chuẩn

CHÚ THÍCH 4: Các bước từ 5 đến 8 giải
công thức chuẩn sử dụng thừa số Cholesky. Một cách tiếp cận bằng số ổn định hơn
là sử dụng thừa số QR [10] của 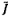 (xem A.5.1). Quy trình mô tả trong C.2
sử dụng thừa số QR và tránh các tính toán liên quan đến số nghịch đảo L
như nêu trong bước 4.
(xem A.5.1). Quy trình mô tả trong C.2
sử dụng thừa số QR và tránh các tính toán liên quan đến số nghịch đảo L
như nêu trong bước 4.
CHÚ THÍCH 5: Về mặt ma trận,
ma trận hiệp phương sai gắn với các ước lượng a và b là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
CHÚ THÍCH 6: Một cách tiếp cận tổng
quát hơn và ổn định hơn bằng số để giải
quyết vấn đề hồi quy Gauss-Markov tổng quát được nêu trong C.2. Cách tiếp cận ở trên giả định
rằng ma trận U là hoàn toàn dương và không thể hiện bất kỳ mối tương
quan mạnh nào.
CHÚ THÍCH 7: u2(a), u2(b) và cov(a,b) trong bước
11 thu được bằng cách áp dụng định luật lan truyền độ không đảm bảo trong TCVN
9595-3:2013 (ISO/IEC Guide 98-3:2008) cho a và b như cung cấp
bởi các bước từ 1 đến 10.
10.2.3 Thực tế là
các ước lượng a và b xác định bằng
cách tối thiểu hóa tổng bình phương
(14) phụ thuộc phi tuyến vào dữ liệu xi và yi nghĩa là
không thể dễ dàng nêu ra các tính chất đối với GGMR. Các ước lượng a và b
xác định trong 10.1.4 có các tính chất sau đây đối với dữ liệu xi và yi theo mô hình
(13):
i) Các ước lượng a và b được cho bởi
hàm phi tuyến các dữ liệu xi và yi.
ii) Các ước lượng a và b có thể được
coi là các thể hiện của biến ngẫu nhiên có kỳ vọng tương ứng là A* và B*.
iii) Các thành phần của ma trận hiệp
phương sai đối với biến ngẫu nhiên trong ii) được lấy xấp xỉ bởi u2(a), u2(b) và cov(a,b) tính được
trong 10.2.2.
Các xấp xỉ ở trên sẽ chính
xác hơn đối với dữ liệu có độ không đảm bảo kèm theo nhỏ hơn. Tuy nhiên, phương
pháp ước lượng có tính chất nhất quán sau đây:
iv) Đối với dữ liệu thỏa mãn mô hình
(13), khi số m điểm dữ liệu tăng thì các ước lượng a và b hội tụ A*
và B*, tương ứng [16].
Nếu đưa ra giả định bổ sung rằng di và ei là thể hiện
của biến ngẫu nhiên đặc trưng bởi phân bố chuẩn nhiều chiều thì khi đó các tính
chất khác gắn với phương pháp ước lượng GGMR có thể đưa ra:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
vi) Các ước lượng a và b là ước lượng
hợp lý lớn nhất, tương ứng với giá trị hợp lý nhất của A và B, có
thể làm tăng dữ liệu đo quan trắc được xi và yi.
vii) Trong bối cảnh suy luận Bayes,
phân bố trong phạm vi kiến thức cho A và B, đã cho dữ liệu đo quan
trắc xi và yi, xấp xỉ phân
bố chuẩn hai chiều tập trung ở
a và b với ma trận
hiệp phương sai xác định bởi u2(a), u2(b) và cov(a,b).
10.3 Xác nhận
giá trị sử dụng của mô hình
Nếu m > 2 thì
giá trị sử dụng của mô hình có thể kiểm nghiệm một phần bằng cách sử dụng phần
dư 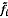 có trọng số
(tiếp theo 10.2.2):
có trọng số
(tiếp theo 10.2.2):
12 Thiết lập giá
trị Khi-bình phương quan trắc được 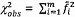 và bậc tự do n = m - 2;
và bậc tự do n = m - 2;
13 Kiểm tra xem
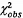 có vượt quá
phân vị 95 % của
có vượt quá
phân vị 95 % của 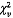 không, và xem liệu có bác bỏ mô hình đường
thẳng hay không.
không, và xem liệu có bác bỏ mô hình đường
thẳng hay không.
CHÚ THÍCH: Kiểm nghiệm Khi-bình phương
dựa trên giả định là di và ei trong mô hình (13) là
các thể hiện của biến
ngẫu nhiên đặc trưng bởi phân bố chuẩn nhiều chiều và dựa trên xấp xỉ bậc một.
VÍ DỤ: Bảng 25 đưa ra bảy điểm dữ liệu
đo được (xi,
yi) thu được bằng
cách sử dụng các mô hình đo mô tả trong D.2 và D.4.
Ma trận hiệp phương sai gắn với yi được rút ra bằng
cách sử dụng mô hình đo (D.1) với uS = 2,0 và uR = 1,0.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Bảng 25 - Dữ
liệu thể hiện bẩy điểm đo, xi và yi có ma trận
hiệp phương sai kèm theo
xi
yi
50,4
52,3
99,0
97,8
149,9
149,7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
200,1
248,5
250,4
299,7
300,9
349,1
349,2
Ma trận hiệp phương sai Ux
kích thước 7
x 7 gắn với xi là

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

Ma trận hiệp phương sai Uy
kích thước 7
x 7 gắn với yi
là

Thừa số Cholesky Ly kích thước 7 x 7 của Uy = LyLyT, tính được sử
dụng một trong hai thuật toán mô tả trong A.4.1, là

Ma trận hiệp phương sai U kích thước
14
x 14 được cho bởi

CHÚ THÍCH: Đối với ví dụ này, có mối
tương quan gắn với từng cặp xi và xj và từng cặp yi
và yj nhưng không có mối tương quan gắn với cặp xi và yi, tức là,
cov(xi, yi) = 0 đối với
mọi i và j.
Thừa số Cholesky L kích thước
14
x 14 được cho bởi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Bình phương tối thiểu có trọng số khớp
với dữ liệu (bước 1 đến 5 trong 6.2.1) cho các xấp xỉ 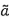 = 0,270 7 và
= 0,270 7 và 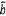 = 1,001 1. Quy trình lặp bắt đầu với
= 1,001 1. Quy trình lặp bắt đầu với 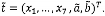 .
.
Bảng 26 đưa ra véc tơ ban đầu 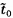 , các hiệu chính δtk = đối với lần
lặp thứ k, k = 1,...,4 và
ước lượng cuối
, các hiệu chính δtk = đối với lần
lặp thứ k, k = 1,...,4 và
ước lượng cuối 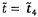 .
.
Bảng 26 -
Thay đổi véc tơ tham
số 






...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
17.253 1
1.258 0
3.078 2
0.290 4
50.572 7
99.000 0
-43.150 1
-3.214 5
-6.320 1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
98.568 2
149.900 0
-29.164 1
-3.960 4
-3.888 9
-0.756 4
149.608 0
200.400 0
2.967 7
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-0.602 4
-1.716 5
200.428 6
248.500 0
24.039 4
-11.406 4
3.237 8
-1.706 4
248.739 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-22.251 0
-15.776 7
-3.358 1
-2.611 0
299.475 9
349.100 0
-20.619 2
-16.621 7
-3.380 5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
348.892 1
0.270 7
7.504 0
-33.395 7
0.100 6
-5.301 9
0.342 4
1.001 1
0.011 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.007 6
0.033 7
1.001 2
Các ước lượng tốt nhất của A và B
là a = 0,342 4 và b = 1,001 2.
Ở lần lặp cuối ma trận M kích
thước 9 x 9 là

như vậy M22(10.2.2 bước
11) là

Độ không đảm bảo chuẩn và hiệp phương
sai gắn với a và b được đánh giá trong bước 11 của 10.2.2 là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Giá trị Khi-bình phương quan trắc được
là 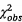 = 1,772 với n = 5 bậc tự do, như tính được trong
bước 12 ở 10.3. Vì
= 1,772 với n = 5 bậc tự do, như tính được trong
bước 12 ở 10.3. Vì 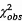 không vượt quá phân vị
95 % của
không vượt quá phân vị
95 % của 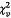 , tức là
11,070, nên không có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và
dữ liệu.
, tức là
11,070, nên không có lý do để nghi ngờ sự nhất quán của mô hình đường thẳng và
dữ liệu.
11 Sử dụng hàm hiệu
chuẩn
Việc sử dụng hàm hiệu chuẩn để dự đoán và
đánh giá tiếp là độc lập với phương pháp được dùng để ước lượng tham số hàm hiệu
chuẩn và đánh giá độ không đảm bảo chuẩn và hiệp phương sai kèm theo.
11.1 Dự đoán
11.1.1 Xét nội dung
dưới đây được quy định, sau khi áp dụng một trong các điều từ 6 đến 10:
a) ước lượng tham số đường thẳng a
và b, độ không đảm bảo chuẩn u(a) và u(b) và hiệp phương
sai cov(a,b) gắn với a
và b, và
b) giá trị đo được y của Y
và độ không đảm bào chuẩn kèm theo u(y).
Coi là y thu được độc lập với dữ liệu
đo sử dụng để thiết lập hàm hiệu chuẩn.
11.1.2 Ước lượng x của
X tương ứng với
y là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
(15)
11.1.3 Độ không đảm
bảo chuẩn u(x) gắn với x được cho bởi

CHÚ THÍCH 1: Công thức cho u2(x)
được thiết lập bằng cách sử dụng định luật lan truyền độ không đảm bảo trong
TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008). Xấp xỉ được dựa trên tuyến tính hóa công thức
(15). c(a), c(b) và c(y) đại diện cho hệ số độ nhạy.
CHÚ THÍCH 2: Công thức ma trận có thể
thuận lợi cho mục đích tính toán:

CHÚ THÍCH 3: Trong trường hợp b = 0, tức là,
đường thẳng khớp nhất Ià y = a, tương ứng với hàm
hiệu chuẩn không chấp nhận được, thì không thể tiến hành dự đoán.
CHÚ THÍCH 4: Giá trị sử dụng của độ
không đảm bảo chuẩn u(x) phụ thuộc vào sự thỏa mãn của kiểm nghiệm Khi-bình phương
liên quan được nêu trong các điều từ 6 đến 10.
VÍ DỤ 1: Xét ví dụ số về bình phương tối
thiểu có trọng số (WLS) có trọng số đã biết bằng nhau mô tả trong Điều
6, tham số đường thẳng khớp nhất và độ không đảm bảo chuẩn, hiệp phương sai kèm
theo là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Lấy y = 10,5 là giá trị đo được
bổ sung của Y
và độ không đảm bảo chuẩn kèm theo u(y) = 0,5.
Từ 11.1.2, ước lượng giá trị x của
X tương ứng với y là
x = (10,5 -
1,867)/1,757 = 4,913.
Sử dụng 11.1.3, độ không đảm bảo chuẩn
kèm theo u(x) được cho bởi

VÍ DỤ 2: Xét ví dụ số về
bình phương tối
thiểu có trọng số (WLS) có trọng số không bằng nhau
đã biết mô tả ở Điều 6, tham số đường
thẳng khớp nhất và độ không đảm bảo chuẩn, hiệp phương sai kèm theo là
a = 0,885, b = 2,057, u(a) = 0,530, u(b) = 0,178, cov(a,b) = -0,082.
Lấy y = 10,5 là giá trị đo được
bổ sung của Y và độ không đảm bảo chuẩn kèm theo u(y) = 1,0.
Từ 11.1.2, ước lượng giá
trị x của X tương ứng với y là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Sử dụng 11.1.3, độ không đảm bảo chuẩn
kèm theo u(x) được cho bởi

Trong ví dụ này và Ví dụ 1 ở 11.1, ảnh hưởng
của các độ không đảm bảo khác nhau gắn với giá trị của y có thể được thấy trong
độ không đảm bảo tương ứng gắn với giá trị tương ứng của x.
11.2 Đánh
giá tiếp
Xét nội dung dưới đây được quy định,
sau khi áp dụng một trong các điều từ 6 đến 10:
a) ước lượng tham số đường thẳng a
và b, độ không đảm bảo chuẩn u(a) và u(b) và hiệp phương
sai cov(a,b) gắn với a và b, và,
b) giá trị đo được x của X và độ không đảm
bảo chuẩn kèm theo u(x).
Coi là x thu được độc lập với dữ
liệu đo sử dụng để thiết lập hàm hiệu chuẩn.
11.2.1 Ước lượng y
của Y tương ứng với x là
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
(16)
11.2.2 Độ không đảm
bảo chuẩn u(y) gắn với y được cho bởi

CHÚ THÍCH 1: Công thức cho u2(y)
được thiết lập bằng cách sử dụng định luật lan truyền độ không đảm bảo trong
TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008). Xấp xỉ được dựa trên tuyến tính hóa công thức (16).
c(a), c(b) và c(y) đại diện cho hệ số độ nhạy.
CHÚ THÍCH 2: Công thức ma trận có thể thuận lợi
cho mục đích tính toán:

CHÚ THÍCH 3: Giá trị sử dụng của độ
không đảm bảo chuẩn u(y) phụ thuộc vào sự thỏa mãn của kiểm
nghiệm Khi-bình phương liên quan được
nêu trong các điều từ 6 đến 10.
VÍ DỤ: Xét ví dụ số về bình phương tối
thiểu có trọng số (WLS) có trọng số đã biết bằng nhau mô tả trong Điều
6, tham số đường thẳng khớp nhất và độ không đảm bảo chuẩn, hiệp phương sai kèm
theo là
a = 1,867, b = 1,757, u(a) = 0,465, u(b)
= 0,120, cov(a,b) = -0,050.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Từ 11.2.1, ước lượng giá trị y
của Y tương ứng với x là
y = 1,867 +
(1,757)(3,5) = 8,017.
Sử dụng 11.2.2, độ không đảm bảo chuẩn
kèm theo u(y) được cho bởi

như vậy u(y) = 0,406.
Phụ
lục A
(tham
khảo)
Phép tính ma trận
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ lục này mô tả các phép tính ma trận
được sử dụng trong tiêu chuẩn này.
A.2 Phép tính cơ
bản
Trong các phép tính sau đây, A
là ma trận kích thước m x n với phần tử A(i, j) = aij trong hàng
thứ i và cột thứ j,
B là ma trận kích thước n x k, C là ma trận
(vuông) kích thước m x m và d là véc tơ kích thước n x
1 với phần tử thứ j dj.
A.2.1 Phép nhân ma
trận-véc tơ
Tích ma trận-véc tơ Ad là véc
tơ e kích thước m x 1 với phần tử thứ i ei xác định bởi

A.2.2 Phép nhân ma
trận-ma trận
Tích ma trận AB là ma trận
kích thước m x k có cột thứ j
là tích của A và cột thứ j của B.
A.2.3 Chuyển vị ma
trận
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
A.2.4 Ma trận đơn
vị
Ma trận đơn vị bậc m là ma trận
I kích thước m x m sao cho I(j, j) = 1, j = 1,…, m, và tất cả các phần tử khác bằng 0.
A.2.5 Nghịch đảo ma
trận vuông
Nghịch đảo của C, nếu có, được ký hiệu
là C-1 và là ma trận
kích thước m x m sao cho

Chuyển vị của C-1 bằng nghịch
đảo của CT
và được ký hiệu là C-T.
A.3 Các định
nghĩa cơ bản
Trong các định nghĩa sau đây, C
là ma trận (vuông) kích thước m x m với phần tử C(i, j) = cij trong hàng
thứ i và cột thứ j.
A.3.1 Ma trận đối
xứng
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
A.3.2 Ma trận khả
nghịch
Ma trận C là khả nghịch
nếu tồn tại nghịch đảo C-1 của nó (xem
A.2.5).
A.3.3 Ma trận tam
giác dưới và tam giác trên
Ma trận C là ma trận tam giác
dưới nếu cij = 0, i
< j, và ma trận tam giác trên nếu cij = 0, i > j.
A.3.4 Ma trận trực
giao
Ma trận C là trực giao
nếu CTC = I.
A.4 Thừa số
Cholesky
Thừa số Cholesky của ma trận hoàn toàn
dương đối xứng U kích thước m x m là ma trận
tam giác dưới L kích thước m x m sao cho U
= LLT [10].
A.4.1 Thuật toán
thừa số Cholesky
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

CHÚ THÍCH: Để ghi đè các
phần tử tam giác dưới U(i,
j),
i ≥ j của U
với thừa số Cholesky của nó, chỉ thực hiện các bước trong giai đoạn Thừa số hóa của
thuật toán trong A.4.1.1, sử dụng U thay cho L.
A.4.1.2 Các tính
toán trong A.4.1.1 có thể được tổ chức lại để liên quan nhiều phép tính véc
tơ-véc tơ hơn nhằm cải thiện tốc độ thực hiện trong ngôn ngữ máy tính hỗ trợ
các phép tính véc tơ và mảng. Ví dụ

CHÚ THÍCH: Để ghi đè các phần tử tam
giác dưới U(i,
j),
i ≥ j của U với thừa số Cholesky
của nó, chỉ thực hiện các bước trong giai đoạn Thừa số hóa của thuật
toán trong A.4.1.2, sử dụng U thay cho L.
A.4.2 Giải thích
phép thừa số hóa Cholesky của ma trận hiệp phương sai
A.4.2.1 Giả định Ei,
i = 1,…,
m là
m biến ngẫu nhiên độc lập, mỗi biến có kỳ vọng bằng 0 và phương sai bằng 1, lấy
ei là thể hiện của Ei. Lấy

Khi đó, 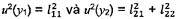 . Sự phụ thuộc chung của y1 và y2 vào ei nghĩa là y1 và y2 có mối tương quan,
với hiệp phương sai cov(y1, y2) = l11l21. Tiếp tục,
giả định
. Sự phụ thuộc chung của y1 và y2 vào ei nghĩa là y1 và y2 có mối tương quan,
với hiệp phương sai cov(y1, y2) = l11l21. Tiếp tục,
giả định
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
A.4.2.2 Theo thuật ngữ
ma trận, y = Le, với tam giác dưới L. Sự phụ thuộc
chung của y1 và y3 vào e1 nghĩa là có
mối tương quan gắn với y1 và y3. Tương tự, sự
phụ thuộc chung của y2 và y3 vào e1 và e2 nghĩa là có mối
tương quan gắn với y2 và y3, và cứ tiếp
như vậy.
A.4.2.3 Cho trước ma
trận hiệp phương sai U gắn với dữ liệu yi, thừa số
Cholesky U = LLT tính các hệ số Iij sao cho ma
trận hiệp phương sai có thể giải thích bằng cách giả định rằng yi
được định nghĩa trong A.4.2.1 như thể hiện của các tổ hợp tuyến tính xác định bởi
Iij của các biến
ngẫu nhiên độc lập Ei. Trên thực tế, các ma trận hiệp phương
sai thường được xác định về các thừa số U = BBT và U
đã cho có vô cùng nhiều
thừa số B có thể sử dụng để xây dựng U. Thừa số Cholesky,
trong đó các tổ hợp tuyến tính được đại diện bởi ma trận tam giác dưới, là duy
nhất đến dấu trị số của các cột của L.
A.4.3 Giải hệ tam giác dưới
A.4.3.1 Nếu L
là ma trận tam giác dưới kích thước m x m sao cho L(j, j) ≠ 0, j = 1,…, m và x
là véc tơ kích thước m x 1, thuật toán sau đây tính véc tơ y, trong đó y sao cho Ly = x, tức là, y = L-1x.

CHÚ THÍCH: Để ghi đè véc tơ x với lời
giải y, chỉ thực hiện
các bước trong giai đoạn Giải của thuật toán trong A.4.3.1, sử dụng x
thay cho y.
A.4.3.2 Thuật toán
trong A.4.3.1 có thể áp dụng để giải phương trình ma trận LY = X bằng cách áp dụng
liên tiếp cho từng cột của X. Về toán học, lời giải được cho bởi Y = L-1X.
A.4.4 Giải hệ tam
giác trên
A.4.4.1 Phép giải hệ
tam giác trên có thể được xác định theo chuyển vị ma trận tam giác dưới. Nếu L là
ma trận tam giác dưới kích thước m x m sao cho L(j, j) ≠ 0, j = 1,..., m và x là véc tơ kích
thước m
x
1, thuật toán sau đây tính véc tơ y, trong đó y sao cho LTj = x, tức Ià, y = L-Tx.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

CHÚ THÍCH: Để ghi đè véc tơ x với lời giải
y, chỉ thực hiện
các bước trong giai đoạn Giải của thuật toán trong A.4.4.1, sử dụng x thay cho y.
A.4.4.2 Thuật toán
trong A.4.4.1 có thể áp dụng để giải phương trình ma trận LTY = X bằng
cách áp dụng liên tiếp cho từng cột của X. Về toán học, lời
giải được đưa ra bởi Y = L-1X.
A.5 Thừa số trực
giao
Các ma trận trực giao là tổ hợp các phép
quay và phép đối xứng và có tính chất nhân trước véc tơ với ma trận trực giao mà không
làm thay đổi độ lớn của véc tơ đó (căn bậc hai tổng các bình phương các phần tử của nó). Các
cột của ma trận trực giao có thể được coi như xác định hệ trục vuông góc. Điều
quan trọng của kỹ thuật thừa số trực giao là nó cho phép giải các phương trình
ma trận theo cách số học ổn định. Các thuật toán để tính thừa số trực
giao được mô tả trong các tài liệu tham khảo [1,10, 20].
A.5.1 Thừa số QR
Thừa số QR của ma trận A kích
thước m
x
n, với m ≥ n, có thể được viết
là

trong đó Q = [Q1 Q2] là ma trận
trực giao kích thước m x m, Q1
là ma trận bao gồm n cột đầu tiên
của Q, với 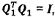 ,
và R1 là ma trận
tam giác trên kích thước n x n.
,
và R1 là ma trận
tam giác trên kích thước n x n.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
A.5.2 Thừa số RQ
A.5.2.1 Thừa số RQ của
ma trận B kích thước m x n, với m ≥ n có thể được
viết là

trong đó Z là ma trận trực giao
T2 là ma trận tam
giác trên.
A.5.2.2 Thừa số RQ của
ma trận B kích thước m x n, với m < n có thể được
viết là

trong đó Z là ma trận trực giao
T2 là ma trận
tam giác trên.
Phụ
lục B
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Áp dụng thuật toán Gauss-Newton cho hồi quy
khoảng cách tổng quát
B.1 Phụ lục này
rút ra các thuật toán trong 7.2.1 và 8.2.1 bằng cách sử dụng thuật toán Gauss-Newton.
B.2 Các thuật
toán trong 7.2.1 và 8.2.1 là ứng dụng cụ thể của thuật toán Gauss-Newton lặp
[10] để tối thiểu hóa tổng
các bình phương của hàm phi tuyến:

B.3 Lấy 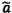 là xấp xỉ của các tham số
giải a và
là xấp xỉ của các tham số
giải a và

tương ứng là véc tơ kích thước m x 1 của các
giá trị hàm số và ma trận Jacobi kích thước m x n của đạo hàm
riêng bậc một đối với các tham số, đánh giá tại 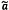 xấp xỉ với các tham số.
xấp xỉ với các tham số.
B.4 Lấy p
giải

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
B.5 Đối với các
thuật toán trong 7.2.1 và 8.2.1, a = (A, B)T và hàm ƒi(A) là thước đo
khoảng cách tổng quát tính từ điểm dữ liệu thứ i(xi, yi) đến đường y
- A + Bx.
B.6 Lấy Ui là ma trận
hiệp phương sai gắn với điểm dữ liệu thứ i:

và lấy 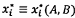 , gọi là điểm chân thứ i, giải
, gọi là điểm chân thứ i, giải

(B.2)
hàm của A và B.
B.7 Nếu 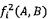 được xác định bằng
được xác định bằng

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

xác định đường hồi quy khoảng cách tổng
quát khớp nhất. Áp dụng thuật toán Gauss-Newton đòi hỏi xác định đạo hàm riêng
bậc một của ƒi(A, B) đối với A và
B để hình thành
ma trận Jacobi J.
B.8 Lấy n = (-B,1)T
là véc tơ trực giao với đường y = A + Bx và giả định rằng 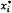 là phép giải của vấn đề
điểm chân (B.2). Đặt
là phép giải của vấn đề
điểm chân (B.2). Đặt 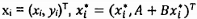 và
và

(B.3)
khi đó, biểu thị giá trị hàm và đạo
hàm đối với Ui, A, B, xi, yi và 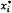 ,
,

(B.4)
và
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
(B.5)
B.9 Giải 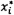 của vấn đề điểm chân
(B.2) được cho bởi
của vấn đề điểm chân
(B.2) được cho bởi

(B.6)
CHÚ THÍCH: Biểu thức (B.3), (B.4),
(B.5) và (B.6) được xác định đối với Ui chứ không phải nghịch
đảo của 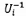 ,. Không có yêu
cầu Ui khả nghịch nhưng nTUin phải khác
không.
,. Không có yêu
cầu Ui khả nghịch nhưng nTUin phải khác
không.
B.10 Các thuật
toán trong 7.2.1 và 8.2.1 áp dụng thuật toán Gauss-Newton sử dụng các biểu thức
rõ ràng cho
ƒi(A,B), 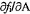 và
và 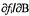 . Giải cho bước mới p trong
biểu thức (B.1) được hình thành như vấn đề xác định đường thẳng khớp nhất bình
phương tối thiểu có trọng số (xem 6.2.1 các bước từ 1 đến 5) đối với dữ liệu
chuyển đổi rút ra từ dữ liệu đo (xi,yi), ma trận hiệp
phương sai kèm theo Ui và các gần đúng hiện tại với A
và B.
. Giải cho bước mới p trong
biểu thức (B.1) được hình thành như vấn đề xác định đường thẳng khớp nhất bình
phương tối thiểu có trọng số (xem 6.2.1 các bước từ 1 đến 5) đối với dữ liệu
chuyển đổi rút ra từ dữ liệu đo (xi,yi), ma trận hiệp
phương sai kèm theo Ui và các gần đúng hiện tại với A
và B.
Phụ
lục C
(tham
khảo)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
C.1 Khái quát
Thuật toán lặp mô tả trong 10.2.2 giả định
rằng ma trận hiệp phương sai U kích thước 2m x 2m là xác định
dương và do đó là khả nghịch. Đặc biệt, tính khả nghịch đòi hỏi mọi u(xi)
> 0 và u(yi) > 0. Trong phụ lục này thuật toán
tổng quát được mô tả là phù hợp cho mọi ma trận hiệp phương sai U
(bán xác định dương đối xứng). Tất cả những gì được yêu cầu là ma
trận hiệp phương sai có thể thừa số hóa là U = BBT,
trong đó B là ma trận kích thước 2m x p (p ≥ m). Thông thường,
ma trận hiệp phương sai được bắt nguồn từ thừa số hóa như vậy. Nếu U
là khả nghịch thì B có thể là thừa số Cholesky của nó. Thuật toán
tiến hành tương tự như mô tả trong 10.2.2 và yêu cầu tính toán số dư ƒ và ma trận
Jacobi J, nhưng số gia δt được xác định bằng cách sử dụng hai thừa
số trực giao, về toán học, δt tối thiểu hóa

C.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn, hiệp phương sai kèm theo
Các ước lượng a và b được
tính như trong các bước từ 1 đến 9 dưới đây; độ không đảm bảo chuẩn u(a) và
u(b) được đánh giá trong bước 10:
1 Thu được các
xấp xỉ ban đầu 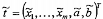 cho tham số;
cho tham số;
2 Tính véc tơ
kích thước 2m x 1,

và ma trận (Jacobi) kích thước 2m x
(m + 2),
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
trong đó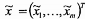 được trích từ ước lượng
được trích từ ước lượng 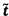 hiện tại của véc tơ tham số;
hiện tại của véc tơ tham số;
3 Xác định thừa
số QR của J:

trong đó Q là ma trận trực
giao, kích thước 2m x 2 m và R1 là ma trận
tam giác trên kích thước (m + 2) x (m + 2); xem A.5.1;
4 Hình thành
tích ma trận QTB và xác định thừa số RQ của nó
QTB = TZ,
trong đó T là ma trận,
kích thước 2m x
p và Z
là ma trận trực giao kích thước p x p; xem A.5.2;
5 Đặt 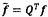 và phân vùng
và phân vùng 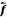 và T.
và T.

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
6 Giải hệ tam
giác trên 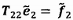 để xác định
véc tơ
để xác định
véc tơ 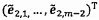 kích thước (m - 2) x 1;
xem A.4.4;
kích thước (m - 2) x 1;
xem A.4.4;
7 Giải hệ tam
tác trên 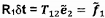 để xác định số
gia
để xác định số
gia 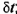 , xem A.4.4;
, xem A.4.4;
8 Cập nhật các
xấp xỉ hiện tại cho các tham
số: 
9 Lặp lại các
bước từ 2 đến 8 cho đến khi đạt được sự hội tụ. Đặt 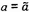 và
và 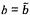 (các thành phần m + 1 và m + 2
của
(các thành phần m + 1 và m + 2
của 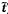 );
);
10 Lấy Ra
là ma trận dưới bên phải kích thước 2 x 2 của R1 và Ta
là ma trận dưới bên phải kích thước 2 x 2 của T11. Giải hệ tam
giác trên

đối với ma trận tam giác trên Ka
kích thước 2
x 2 (xem A.4.4)
và đặt Ua = KaKaT. Khi đó

CHÚ THÍCH 1: Cách tiếp cận mô tả trong
C.2 đại diện cho cách giải tổng quát nhất để xác định hàm hiệu chuẩn tuyến tính sử dụng
phương pháp bình phương tối thiểu. Tất cả các cách tiếp cận khác mô tả trong tiêu chuẩn
này có thể được giải
như trường hợp đặc biệt.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
C.3 Xác nhận giá
trị sử dụng của mô hình
Nếu m > 2 thì giá trị sử dụng
của mô hình có thể kiểm nghiệm một phần bằng cách sử dụng thành phần véc tơ 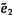 (tiếp theo C.2):
(tiếp theo C.2):
11 Thiết lập giá
trị Khi-bình phương quan trắc được 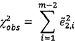 và bậc tự do n = m - 2;
và bậc tự do n = m - 2;
12 Kiểm tra xem 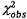 có vượt quá phân
vị 95 % của
có vượt quá phân
vị 95 % của 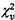 không,
và xem liệu có bác bỏ mô hình đường thẳng hay không.
không,
và xem liệu có bác bỏ mô hình đường thẳng hay không.
CHÚ THÍCH: Kiểm nghiệm Khi-bình phương dựa
trên giả định là di và ei trong mô hình (13) là
các thể hiện của biến ngẫu nhiên đặc trưng bởi phân bố chuẩn nhiều chiều và dựa
trên xấp xỉ bậc một.
Với giả định này,
véc tơ 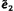 kích thước (m
- 2) x 1 gắn với phân bố Gauss nhiều chiều có ma trận hiệp phương sai bằng với
ma trận đơn vị kích thước (m
- 2) x (m - 2) sao cho
kích thước (m
- 2) x 1 gắn với phân bố Gauss nhiều chiều có ma trận hiệp phương sai bằng với
ma trận đơn vị kích thước (m
- 2) x (m - 2) sao cho
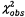 gắn với phân bố x2 với m
- 2 bậc tự do.
gắn với phân bố x2 với m
- 2 bậc tự do.
VÍ DỤ 1: Cách tiếp cận thừa số QR có
thể áp dụng cho ví dụ số mô tả
trong Điều 10.
Ma trận hiệp phương sai Ux
sinh ra dưới dạng thừa số (xem D.4) là
Ux = BxBxT,
trong đó
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Ma trận hiệp phương sai Uy =
ByByT cũng có dạng thừa số với

Ma trận hiệp phương sai U
hoàn chỉnh kích thước 14 x 14 được thừa số hóa thành U = BBT,
trong đó B là ma trận kích
thước 14 x 18

Đối với ví dụ này, thuật toán trong
C.2 tương đương về toán học với thuật toán trong 10.2.2 và hai cách tiếp cận đều
cho kết quả số rất giống nhau.
VÍ DỤ 2: Bảng C.1 cho 7 điểm dữ liệu
đo được (xi, yi) thu được bằng
cách sử dụng mô hình đo mô tả trong D.2 và D.5.
Ma trận hiệp phương sai gắn với yi
được rút ra bằng cách sử dụng mô hình (D.1) với uS = 2,0 và uR
= 1,0 và giống như trong Ví dụ 1 Phụ lục C.
Dữ liệu xi và ma trận
hiệp phương sai kèm theo được rút ra bằng cách sử dụng mô hình đo (D.3) với z1 = 50, z2 = 100, z3 = 200, u(z1) = 0,5 và u(z2) = u(z3) = 1,0, sao
cho
Ux = BxBxT,
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

Ma trận hiệp phương sai hoàn chỉnh U kích thước 14 x 14 được thừa
số hóa thành U = BBT, trong đó B
là ma trận kích thước 14 x 11

Đối với ví dụ này, không thể áp dụng
thuật toán trong 10.2.2 vì U không xác định dương. Thay vào đó có thể sử dụng
thuật toán mô tả trong C.2.
Bảng C.2 đưa ra véc tơ ban đầu  , các hiệu
chính
, các hiệu
chính 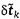 = đối với lần
lặp thứ k,
k
=
1,...,5 và ước lượng cuối
= đối với lần
lặp thứ k,
k
=
1,...,5 và ước lượng cuối 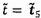 .
.
Bảng C.1 - Dữ
liệu thể hiện 7 điểm đo, xi và yi
có ma trận hiệp phương sai kèm theo
xi
yi
50,5
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
99,7
98,4
150,2
153,7
199,5
194,0
249,9
251,9
299,2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
349,7
349,0
Bảng C.2 -
Thay đổi véc tơ tham số 






...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
50.500 0
99.700 0
150.200 0
199.500 0
249.900 0
299.200 0
349.700 0
30.822 9
55.831 3
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-59.071 1
-28.248 2
-3.239 8
27.583 1
3.187 4
-13.836 5
-10.649 1
-45,597 6
-45.410 2
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-59.246 7
23.295 7
26.113 6
49.409 3
-49.584 9
-26.289 1
-23.471 3
0,175 5
8.112 4
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7.906 1
-44.790 4
-36.678 0
-44.996 7
-36.884 3
16.423 1
15.677 0
32.100 2
-43.047 0
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-27.369 8
-10.946 8
50.808 0
100.257 0
151.065 5
198.904 4
249.613 0
299.161 3
349.969 9
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.004 2
-50.620 3
0,173 8
-140.085 6
0.857 1
-63.931 6
0.321 7
-100.943 2
0.610 8
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
0.372 2
-2.373 1
1.006 0
Phụ
lục D
(tham
khảo)
Quy định về độ không đảm bảo và hiệp phương
sai gắn với x-giá trị và y-giá trị đo được
D.1 Khái quát
Phụ lục này chỉ ra cách thức để thu được
độ không đảm bảo và hiệp phương sai gắn với giá trị đo đáp ứng và kích thích đo
được. Cách tiếp cận dựa trên việc sử dụng mô hình đo gồm các quá trình làm cơ sở cho việc xác
định dữ liệu đáp ứng và kích thích, và áp dụng định luật lan truyền độ không đảm
bảo trong TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008). Các ví dụ minh họa được sử
dụng cho mục đích này.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
D.2.1 Khái quát
D.2.1.1 Giả định đại
lượng Y
đại
diện đáp ứng phương tiện đo có thể được biểu thị bằng mô hình đo
Y=Y0 + E,
(D.1)
trong đó Y0 là đại lượng
thể hiện bởi đáp ứng chỉ thị và E là đại lượng đại diện cho ảnh hưởng hệ thống.
Giả định rằng hiểu biết về Y0 được mã hóa bằng phân bố có độ lệch
chuần uR. Phân bố này
thường dựa trên phân tích số lượng chỉ thị lặp lại của Y. Y0 được ước lượng
bằng trung bình của các chỉ thị này và uR là độ không
đảm bảo chuẩn gắn với ước lượng này. Giả định rằng hiểu biết về E sao
cho E có kỳ vọng 0 (tức là, mọi hiệu chính cần thiết đều được áp dụng)
và phương sai 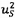 (thu
được từ hiểu biết phụ thuộc vào tính chất cụ thể của phương tiện đo).
(thu
được từ hiểu biết phụ thuộc vào tính chất cụ thể của phương tiện đo).
D.2.1.2 Tiếp sau biểu
thức (D.1), bằng việc áp dụng định luật lan truyền độ không đảm bảo trong TCVN
9595-3:2013 (ISO/IEC Guide 98-3:2008), độ không đảm bảo chuẩn u(yi) gắn với giá
trị đo được yi của Y được cho bởi

Ngoài ra, hiệp phương sai gắn với giá
trị đo được
yi và yj của Y là

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

D.2.2 Mô hình đo
dùng cho độ không đảm bảo và hiệp phương sai gắn với yj
D.2.2.1 Dữ liệu sử dụng
trong ví dụ ở Điều 9 được rút ra từ hệ đo trong đó hai nhóm phép đo được thực
hiện. Mỗi nhóm phép đo chịu một ảnh hưởng hệ thống khác nhau với hai ảnh hưởng
không tương quan, tức là,

trong đó Y0,i là đại lượng
thể hiện bởi đáp ứng chỉ thị thứ i và các đại lượng E1 và E2 đại diện cho
ảnh hưởng hệ thống. Giả định rằng hiểu biết về Y0,i sao cho Y0,i có phương sai 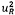 và hiểu biết về Ek sao cho Ek
có kỳ vọng bằng 0 và phương sai
và hiểu biết về Ek sao cho Ek
có kỳ vọng bằng 0 và phương sai 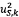 , đối với k = 1, 2.
, đối với k = 1, 2.
D.2.2.2 Độ không đảm
bảo chuẩn u(yi) gắn với giá
trị đo được
yi của Yi được cho bởi

Hiệp phương sai gắn với giá trị đo được yi và yj là

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

D.3 Dữ liệu đáp ứng 2
D.3.1 Mô hình đo giống
như trong biểu thức (D.1) ngoại trừ thay vì ảnh hưởng hệ thống E là tuyệt đối,
D là ảnh hưởng hệ thống
tương đối:
Y= Y0(1 + D).
D.3.2 Xử lý tương
tự như ở D.2 ngoại trừ
là lúc này, sử dụng uD để ký hiệu cho độ không đảm bảo chuẩn
tương đối gắn với ước lượng của Y0,

D.3.3 Ma trận hiệp
phương sai trong trường hợp này là

D.4 Dữ liệu kích
thích 1
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

Các biến ngẫu nhiên Zk,
k = 1,2,3, có các kỳ vọng zk và phương sai u2(zk), trong khi Di
có kỳ vọng bằng 0 và phương sai 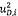 . (Trong hiệu chuẩn khối lượng, giá trị zk
là giá trị đã hiệu chuẩn đối với các khối lượng và u(zk) là độ
không đảm bảo kèm
theo.)
. (Trong hiệu chuẩn khối lượng, giá trị zk
là giá trị đã hiệu chuẩn đối với các khối lượng và u(zk) là độ
không đảm bảo kèm
theo.)
D.4.2 Độ không đảm
bảo u(zk) và u(di) được lan truyền thông
qua mô hình đo trong D.4.1 sang những độ không đảm bảo gắn với các ước
lượng xi của Xi bằng cách sử
dụng định luật lan truyền độ không đảm bảo trong TCVN 9595-3:2013 (ISO/IEC
Guide 98-3:2008). Sự phụ thuộc chung của Xi vào Zk
có nghĩa là một số hiệp phương sai khác không. Sự lan truyền được mô tả dễ nhất
theo thuật ngữ ma trận. Lấy

là ma trận độ nhạy kích thước 7 x 10, trong đó CD = I là ma trận
đơn vị kích thước 7 x 7 và

D.4.3 Lấy SD là ma trận
đường chéo kích thước 7 x 7 với thành phần đường chéo SD(i,i) = uD,i, i = 1,...,7, và Sz là ma trận đường chéo kích thước 3
x 3 với thành phần đường chéo Sz(k,k) = u(zk),
k
= 1,2,3. Đặt

D.4.4 Khi đó, ước
lượng tốt nhất của X được
cho bằng x = Czz kích thước 7 x 1 và ma trận hiệp phương sai kèm
theo kích thước 7 x 7 được cho bởi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Số hạng 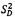 là phương sai đóng góp phát sinh từ Di
trong khi số hạng thứ hai là đóng góp từ Zk.
là phương sai đóng góp phát sinh từ Di
trong khi số hạng thứ hai là đóng góp từ Zk.
D.5 Dữ liệu kích
thích 2
D.5.1 Dữ liệu sử dụng
trong Ví dụ 2 Phụ lục C được rút ra
từ mô hình đo dưới
đây liên quan đến dữ liệu mô tả trong D.4. Dữ liệu kích thích xi là thể hiện
của các biến ngẫu nhiên Xi, i = 1....,7,
xác định đối với biến ngẫu nhiên Zk, k = 1, 2, 3:

Các biến ngẫu nhiên Zk,
có các kỳ vọng zk và phương
sai u2(zk), k = 1, 2, 3.
D.5.2 Độ không đảm
bảo u(zk) được lan truyền thông qua mô hình đo trong D.5.1
sang những độ không đảm bảo gắn với các ước lượng xi của Xi sử dụng định
luật lan truyền độ không đảm bảo trong TCVN 9595-3:2013 (ISO/IEC Guide
98-3:2008). Theo sau ký hiệu của D.4, ước lượng tốt nhất gắn với Xi được cho bởi
x = Czz kích thước 7 x 1 và ma trận hiệp phương sai kèm theo
kích thước 7
x 7 được cho bởi

Trong trường hợp này Ux
là không nghịch đảo được.
D.6 Dữ liệu kích
thích và đáp ứng
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
D.6.2 Giả định X và Y có thể được
biểu thị bằng mô hình đo

(D.4)
trong đó X0, Y0 và T
là các biến ngẫu nhiên độc lập với kỳ vọng x0, y0 và 0, còn
phương sai tương ứng là u2(x0), u2(y0) và u2(t).
D.6.3 Tiếp sau biểu
thức (D.4), bằng cách áp dụng định luật lan truyền độ không đảm bảo trong TCVN
9595-3:2013 (ISO/IEC Guide 98-3:2008), độ không đảm bảo chuẩn u(xi) và u(yi) gắn với giá
trị đo được xi của X và yi của Y
được cho bởi

Ngoài ra, hiệp phương sai gắn với xi và yi
là

D.6.4 Nếu thay X và Y có thể biểu
thị bằng mô hình đo
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hiệp phương sai gắn với xi và yi
là

Phụ
lục E
(tham
khảo)
Độ không đảm bảo đã biết theo hệ số thang đo
E.1 Phụ lục này
mô tả phương pháp để đánh giá độ
không đảm bảo gắn với dữ liệu đo trong trường hợp độ không đảm bảo chỉ được biết
theo hệ số thang đo.
E.2 Tiêu chuẩn
này giả định chung rằng độ không đảm bảo gắn với dữ liệu đo được cung cấp. Đây là
tình huống khi các đại lượng (các biến) liên quan đã được mô tả đặc trưng theo
các nguyên tắc của TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008) và ISO/IEC Guide
98-3:2008/Suppl. 1:2008 [13] về phân bố xác suất. Giá trị đo được cho bằng kỳ vọng
của biến và phương sai gắn với nó được cho bằng phương sai của biến.
CHÚ THÍCH: Đặc biệt, liên quan đến giá
trị đo được y như thể hiện
của biến đặc trưng bởi phân bố t có tham số tỷ lệ s
và bậc tự do n (n >2), độ không đảm
bảo chuẩn gắn với y được cho bởi u(y) = [n/(n - 2)1/2
s, độ lệch chuẩn của phân bố đó.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
E.4 Ước lượng hậu
nghiệm được xác định bằng cách sử dụng cùng các khái niệm như đã sử dụng trong
việc xác nhận giá trị sử dụng của mô hình. Bằng cách đặt thêm giả định rằng dữ
liệu đầu vào là thể hiện của biến phân bố chuẩn nhiều chiều, ước lượng hậu nghiệm
σ
được
chọn sao cho 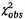 bằng với
m - 2, kỳ vọng của phân bố Khi-bình phương với m - 2 bậc tự do.
Trong trường hợp này không thể tiến hành việc xác nhận giá trị sử dụng của mô hình và dữ liệu
vì ước lượng hậu nghiêm đã được chọn sao cho chuẩn mực hiệu lực được tự động
đáp ứng.
bằng với
m - 2, kỳ vọng của phân bố Khi-bình phương với m - 2 bậc tự do.
Trong trường hợp này không thể tiến hành việc xác nhận giá trị sử dụng của mô hình và dữ liệu
vì ước lượng hậu nghiêm đã được chọn sao cho chuẩn mực hiệu lực được tự động
đáp ứng.
E.5 Do đó,
phương pháp này chỉ nên được sử dụng với chú ý đặc biệt. Ví dụ, nếu đồ thị dữ
liệu chỉ ra rằng hàm hiệu chuẩn đường thẳng không thích hợp thì không nên sử dụng
phương pháp này.
E.6 Các ước lượng
tham số a và b không phụ thuộc vào hệ số thang đo σ. Ước lượng của
σ chỉ yêu cầu để đánh giá độ không đảm bảo chuẩn u(a) và u(b) và hiệp
phương sai cov(a,b) gắn với các
ước lượng này. Đối với trường hợp U đã biết hoàn toàn thì có thể đánh
giá u(a), u(b) và cov(a,b) từ dữ liệu
và U riêng; không cần có giả định về phân bố gắn với dữ liệu. Với giả định
về tính chuẩn, các ước lượng tham số có thể được coi là thể hiện của các biến đặc
trưng bởi phân bố hai chiều nhất định, như dưới đây.
E.7 Trong trường
hợp dữ liệu có thể được coi là thể hiện của phân bố chuẩn nhiều chiều với ma trận
hiệp phương sai U đã biết, phân bố hai chiều trong E.6 là phân bố chuẩn
với ma trận hiệp phương sai Ua có các thành phần u2(a), u2(b) và hiệp
phương sai cov(a,b) như trong biểu thức (1).
E.8 Đối với trường
hợp trong E.4 trong đó phân bố chuẩn nhiều chiều có ma trận hiệp phương sai u
= σ2 U0, trong đó U0 đã biết và σ
chưa biết, thì U0 được sử dụng thay cho U trong
tính toán. Ma trận hiệp phương sai

gắn với các ước lượng của tham số hiệu
chuẩn đường thẳng có thể được tính. Nếu m > 2 thì có thể sử dụng giá trị
Khi-bình phương quan trắc được (xem 6.3) để cung cấp ước lượng hậu nghiệm của hệ
số thang đo gắn với độ không đảm bảo đầu vào. Lấy 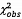 được tính như trong bước 8 của 6.3, và đặt
được tính như trong bước 8 của 6.3, và đặt

E.9 Ma trận hiệp
phương sai điều chỉnh tỷ lệ
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
khi đó được cho bởi

tức là, độ không đảm bảo chuẩn điều chỉnh
tỷ lệ 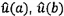 và hiệp phương
sai
và hiệp phương
sai 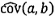 gắn với tham số
khớp được cho bởi
gắn với tham số
khớp được cho bởi

E.10 Các ước lượng
(E.1) được dựa trên việc khớp với một số lượng hữu hạn m điểm dữ liệu và đối với
m nhỏ sẽ ước lượng thấp phương sai của phân bố đối với tham số khớp. Với m >
4, ước lượng tốt hơn được xác định [19, chương 8] bằng cách sử dụng

CHÚ THÍCH: Với giả định về tính
chuẩn, các ước lượng tham số khi đó được gắn với phân bố t hai
chiều với ma trận tỷ lệ 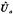 và m - 2 bậc tự do. Với m >
4, ma trận hiệp phương sai của phân bố đó được cho bởi
và m - 2 bậc tự do. Với m >
4, ma trận hiệp phương sai của phân bố đó được cho bởi

(E.2)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
VÍ DỤ: (CHƯA BIẾT TRỌNG SỐ) Trong ví dụ này, xi được lấy là
chính xác và yi có độ không đảm bảo chuẩn bằng nhau nhưng chưa biết,
còn ước lượng hậu nghiệm của độ không đảm bảo gắn với tham số khớp được đánh
giá từ các phần dư của việc khớp. Việc khớp được xác định bằng cách lấy trọng số
bằng 1 (nghĩa là độ không đảm bảo chuẩn u(yi) trên danh nghĩa cũng bằng
1). Dữ liệu được cho trong Bảng E.1.
Bảng E.1 - Dữ
liệu đại diện cho 6 điểm đo, với trọng số đặt bằng 1
xi
yi
u(yi)
1,000
3,014
1
2,000
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1
3,000
7,004
1
4,000
9,061
1
5,000
11,201
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
6,000
12,762
1
Tham số đường thẳng khớp nhất được
tính như trong Bảng E.2. Từ bảng
này, g0 =
21,000/6,000 = 3,500, h0 = 48,267/6,000 =
8,044, b = 34,363/17,500 = 1,964 và a = 8,044 -
(1,964)(3,500) = 1,172.
Bảng E.2 - Bảng tính toán
đi kèm với dữ liệu trong Bảng E.1
w1



...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
hi

gihi
ri

...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
8.044
a = 1.172
1.000
1.000
1.000
3.014
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-5.031
6.250
12.576
-0.122
0.015
1.000
1.000
2.000
5.225
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-2.819
2.250
4.229
0.126
0.016
1.000
1.000
3.000
7.004
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
-1.040
0.250
0.520
-0.059
0.003
1.000
1.000
4.000
9.061
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1.017
0.250
0.508
0.035
0.001
1.000
1.000
5.000
11.201
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
3.157
2.250
4.735
0.211
0.045
1.000
1.000
6.000
12.762
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
4.718
6.250
11.794
-0.191
0.037
6.000
21.000
48.267
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
17.300
34.363
b = 1.964
0.116
Dữ liệu và hàm hiệu chuẩn đường thẳng
khớp được vẽ trên Hình E.1. Số dư có trọng số được minh họa trên Hình E.2. Do u(yi) là tùy ý nên
đưa ra giá trị 1, trong trường hợp này các vạch độ không đảm bảo vượt quá nhiều
các số dư về độ lớn.

Hình E.1 - Dữ
liệu trong Bảng E.1 và hàm hiệu chuẩn đường thẳng khớp thu được trong Bảng E.2
Nếu biết trước là u(yi) = 1, i
= 1,…, m, thì khi đó độ không đảm bảo gắn với các tham số khớp sẽ được tính toán
từ thông tin trong Bảng E.2:
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66

Hình E.2 - Số
dư có trọng số tính bằng cách sử dụng hàm hiệu chuẩn đường thẳng khớp thu được
trong Bảng E.2.
Do các tính toán này dựa trên việc ấn
định tùy ý u(yi) = 1, nên ước
lượng hậu nghiệm 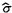 của
u(yi) được yêu cầu
để đánh giá độ không đảm bảo gắn với các tham số khớp. Từ bảng,
của
u(yi) được yêu cầu
để đánh giá độ không đảm bảo gắn với các tham số khớp. Từ bảng,

Giá trị này của 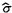 đại diện cho ước lượng của độ
không đảm bảo chuẩn u(yi) gắn với yi
dựa trên giá trị Khi-bình phương quan trắc được. Với ước lượng hậu nghiệm này,
các tính toán có thể lặp lại với u(yi) = 0,171. Các
ước lượng cho a và b sẽ không thay đổi nhưng giá trị Khi-bình
phương quan trắc và độ không đảm bảo sẽ cỏ tỷ lệ như sau:
đại diện cho ước lượng của độ
không đảm bảo chuẩn u(yi) gắn với yi
dựa trên giá trị Khi-bình phương quan trắc được. Với ước lượng hậu nghiệm này,
các tính toán có thể lặp lại với u(yi) = 0,171. Các
ước lượng cho a và b sẽ không thay đổi nhưng giá trị Khi-bình
phương quan trắc và độ không đảm bảo sẽ cỏ tỷ lệ như sau:

như vậy 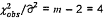 , kỳ vọng của phân bố Khi-bình phương với 4 bậc
tự do. Sử dụng công thức (E.1),
, kỳ vọng của phân bố Khi-bình phương với 4 bậc
tự do. Sử dụng công thức (E.1),

Các thành phần của 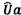 là những thành phần sẽ được đánh
giá nếu đã biết, theo tiên nghiệm, là
là những thành phần sẽ được đánh
giá nếu đã biết, theo tiên nghiệm, là 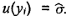 . Tuy nhiên,
. Tuy nhiên, 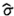 là ước lượng của độ không đảm bảo chuẩn gắn với
yi. Với m
> 4, tỷ lệ tăng của (m - 2)/(m - 4) có thể được kết hợp vào ma trận
hiệp phương sai để tính đến độ không đảm bảo bổ sung phát sinh từ thực
tế
là ước lượng của độ không đảm bảo chuẩn gắn với
yi. Với m
> 4, tỷ lệ tăng của (m - 2)/(m - 4) có thể được kết hợp vào ma trận
hiệp phương sai để tính đến độ không đảm bảo bổ sung phát sinh từ thực
tế 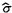 là ước lượng
rút ra từ m điểm dữ liệu. Sử dụng công thức (E.2),
là ước lượng
rút ra từ m điểm dữ liệu. Sử dụng công thức (E.2),
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
như vậy 
Phụ
lục F
(tham
khảo)
Triển khai phần mềm các thuật toán được mô tả
F.1 Việc triển
khai phần mềm các thuật toán mô tả trong tiêu chuẩn này để xác định và
sử dụng hàm hiệu chuẩn đường thẳng đã được Phòng thí nghiệm vật lý quốc gia
(NPL - National Physical Laboratory) ở Anh xây dựng. Phầm mềm có sẵn dưới dạng thư
mục nén ZIP trên trang tin điện tử của NPL tại địa chỉ
www.npl.co.uk/mathematics-scienctific-computing/software-support-for-metrology/software-downloads-(ssfm)
và Tổ chức Tiêu chuẩn hóa Quốc tế tại standards.iso.org/iso/ts/28037/.
F.2 Phần mềm,
phát triển trong ngôn ngữ lập trình MATLAB [18], được cung cấp dưới dạng tệp M
và tệp html xuất bản bằng MATLAB version 7.10.0 (R2010a). Đối với người sử dụng
MATLAB, tệp M có thể chạy trực tiếp và cũng có thể sửa đổi để chạy các
thuật toán đối với các dữ liệu đo khác nhau. Đối với người sử dụng không tiếp cận
được MATLAB, tốt nhất là đọc phần mềm ở dạng tệp html được cung cấp. Có thể sử
dụng phần mềm làm cơ sở cho việc chuẩn bị triển khai các thuật toán trong các ngôn
ngữ lập trình khác. Trong các tệp, các lệnh được thực hiện cho một số hàm
MATLAB cũng bao gồm phần mềm. Ví dụ, hàm algm_gdr1_steps_2_to_5 triển khai các bước 2 đến
5 của quy trình tính toán
cho trường hợp 5.3.2 b) (độ không đảm bảo gắn với giá trị đo được xi và yi
và tất cả các hiệp phương sai gắn với dữ liệu được coi là không đáng kể) quy định
trong 7.2.1. Ngoài ra, một số ứng dụng các chức năng tích hợp của MATLAB được
đưa ra, ví dụ như để thu được thừa số Cholesky của ma trận. Tập lệnh MATLAB (có đuôi '.m')
và tệp html (‘.html’) được cung cấp như sau:
- TS28037_WLS1 chạy ví dụ số về bình
phương tối thiểu có trọng số (WLS) với trọng số bằng nhau đã biết mô tả
trong Điều 6 và thực hiện dự đoán mô tả trong Ví dụ 1 của 11.1 và đánh giá tiếp
mô tả trong 11.2;
- TS28037_WLS2 chạy ví dụ số về bình
phương tối thiểu có trọng số (WLS) với trọng số bằng nhau đã biết mô tả
trong Điều 6 và thực hiện dự đoán mô tả trong Ví dụ 2 của 11.1;
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
- TS28037_GDR1 chạy ví dụ số về hồi
quy khoảng cách tổng quát (GDR) mô tả trong Điều 7;
- TS28037_GDR2 chạy ví dụ số để minh họa
thuật toán cho hồi quy khoảng cách tổng quát (GDR) mô tả trong Điều 8;
- TS28037_GMR chạy ví dụ số về hồi quy
Gauss-Markov (GMR) mô tả trong Điều 9;
- TS28037_GGMR1 chạy ví dụ số về hồi
quy Gauss-Markov tổng quát (GGMR) mô tả trong Điều 10;
- TS28037_GGMR2 chạy ví dụ số về GGMR
mô tả trong Điều 10 và Ví dụ 1 của Phụ lục C sử dụng cách tiếp cận thừa số trực giao mô tả
trong C.2;
- TS28037_GGMR3 chạy ví dụ số về
GGMR mô tả trong Ví dụ 2 của Phụ lục C sử dụng cách tiếp cận thừa số trực giao mô tả
trong C.2;
Trong khi dự đoán và đánh giá tiếp chỉ
thực hiện trong các tập lệnh giải quyết vấn đề WLS, có thể sao chép và dán mã
MATLAB tương ứng với các ứng dụng này của hàm hiệu chuẩn vào bất kỳ tập lệnh
nào được cung cấp.
F.3 Phần mềm cần
được sử dụng cùng với tiêu chuẩn này. Đặc biệt khuyến nghị người sử dụng nghiên
cứu tiêu chuẩn này trước khi chạy phần mềm.
F.4 Phần mềm được
cung cấp với thỏa thuận cấp phép phần mềm (REF: MSC/L/10/001) và việc sử dụng
phần mềm phải tuân thủ các điều khoản được nêu trong thỏa thuận. Bằng việc chạy
mã MATLAB, người sử dụng chấp nhận các điều khoản của thỏa thuận. Các thắc mắc
về phần mềm cần được gửi đến NPL tại địa chỉ enquiries@npl.co.uk.
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ
lục G
(tham
khảo)
Từ vựng ký hiệu chính
A
phần chắn của hàm hiệu chuẩn đường
thẳng
A*
giá trị chưa biết của A đối với một hệ
thống đo cụ thể
a
ước lượng của A
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
véc tơ (a, b)T của ước lượng
tham số
B
độ dốc của hàm hiệu chuẩn đường thẳng
B*
giá trị chưa biết của B đối với một hệ
thống đo cụ thể
b
ước lượng của B
cov(a,b)
hiệp phương sai gắn với a và b
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
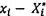 , thể hiện của biến ngẫu nhiên có kỳ vọng bằng
0 và phương sai u2(xi)
, thể hiện của biến ngẫu nhiên có kỳ vọng bằng
0 và phương sai u2(xi)
ei
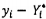 , thể hiện của biến ngẫu nhiên có kỳ vọng bằng
0 và phương sai u2(yi)
, thể hiện của biến ngẫu nhiên có kỳ vọng bằng
0 và phương sai u2(yi)
L
ma trận tam giác dưới
m
số điểm đo được
ri
số dư có trọng số hoặc khoảng cách
có trọng số đối với điểm dữ liệu
thứ i liên quan đến a và b
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
số dư có trọng số hoặc khoảng cách
có trọng số đối với điểm dữ liệu thứ i biểu thị về đại số liên quan đến A
và B
U
ma trận hiệp phương sai kích thước 2m
x 2m gắn với dữ liệu đo (xi, yi), i = 1,…, m
Ua
ma trận hiệp phương sai kích thước 2 x 2 gắn với a
Ux
ma trận hiệp phương sai kích thước m
x m gắn với dữ liệu đo xi, i
= 1,..., m
Uy
ma trận hiệp phương sai kích thước m
x m gắn với dữ liệu đo yi, i = 1,..., m
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
độ lệch chuẩn của biến ngẫu nhiên có
phân bố mã hóa kiến thức về ảnh hưởng ngẫu nhiên
uS
độ lệch chuẩn của biến ngẫu nhiên có
phân bố mã hóa kiến thức về ảnh hưởng hệ thống
u(z)
độ không đảm bảo chuẩn gắn với z,
với z ký hiệu cho a, b, xi, yi, ...
vi
nghịch đảo của u(xi)
wi
nghịch đảo của u(yi)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
biến độc lập (kích thích)
Xi
biến độc lập (kích thích) thứ i

giá trị chưa biết của biến độc lập
(kích thích) thứ i cung cấp bởi
hệ thống đo
x
ước lượng của X (trong trường
hợp dự đoán) hoặc giá trị đo được của X (đánh giá tiếp)
xi
giá trị đo được thứ i của X
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
ước lượng của biến độc lập (kích
thích) thứ i
Y
biến (đáp ứng) phụ thuộc
Yi
biến (đáp ứng) phụ thuộc thứ i

giá trị chưa biết của biến (đáp ứng)
phụ thuộc thứ i cung cấp bởi hệ đo
y
ước lượng của Y (trong trường
hợp dự đoán) hoặc giá trị đo được của Y (đánh giá tiếp)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
giá trị đo được thứ i của Y

ước lượng của biến (đáp ứng) phụ thuộc
thứ i
n
bậc tự do của mô hình, phân bố
Khi-bình phương hoặc phân bố t
σ
độ lệch chuẩn của biến ngẫu nhiên đặc
trưng bởi phân bố xác suất

ước lượng hậu nghiệm của σ
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
giá trị Khi-bình phương quan trắc được

phân bố Khi-bình phương với n bậc tự do
Thư
mục tài liệu tham khảo
[1] Anderson, E.,
Bai, Z., Bischof, C. H.,
Blackford, S., Demmel,
J., Dongarra, J. J., Croz, J. D., I. A. Greenbaum, Hammarling, S., McKenney,
A., and Sorensen, D. C. LAPACK
Users’ Guide, 3rd ed., SIAM, Philadelphia, PA, 1999, http://www.netlib.org/lapack/lug/
[2] Bartholomew-Biggs,
M., Butler, B. P., and
Forbes, A. B. Optimisation algorithms for generalised regression on metrology,
In Advanced Mathematical and Computational Tools in Metrology IV (Singapore,
2000), P. Ciarlini, A. B. Forbes, F. Pavese, and D. Richter, Eds., World
Scienti c, pp. 21-31 (Các thuật toán tối ưu hóa cho hồi quy tổng quát về đo lường,
trong các công cụ toán học và tính toán nâng cao trong đo lường IV)
[3] Boggs, P. T.,
Byrd, R. H., and
Schnabel, R. B. A stable and e cient algorithm for nonlinear orthogonal
distance regression, SIAM J. Sci. Stat. Comput. 8, 6 (1987), 1052-1078 (Thuật
toán ổn định và hiệu quả cho hồi quy khoảng cách trực giao phi tuyến)
[4] Butler, B. P.,
Cox, M. G., Ellison, S. L. R., and
Hardcastle, W. A., Eds., Statistics Software Quali cation: Reference Data Sets,
Royal Society of Chemistry, Cambridge, 1996 (Phần mềm thống kê Quali cation)
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
[6] Cox, M. G.,
Forbes, A. B., Harris, P. M., and Smith, I. M. The classi cation and solution regression
problems for calibration, Tech. Rep. CMSC 24/03, National Physical Laboratory, Teddington,
UK, 2003 (Các cation phân loại và giải pháp cho các vấn đề hồi quy đối với hiệu chuẩn)
[7] Draper, N.
R., and Smith, H. Applied Regression Analysis, Wiley, New York, 1998, Third
edition (Phân tích hồi quy ứng dụng)
[8] Forbes, A.
B., Harris, P. M., and Smith, I. M. Generalised Gauss-Markov regression, In
Algorithms for Approximation IV (Hudders eld, UK, 2002), J. Levesley, I.
Anderson, and J. C. Mason, Eds., University of Hudders eld, pp. 270-277
[9] Fuller, W. A.
Measurement Error Models, Wiley, New York, 1987
[10] Golub, G. H.,
and Van Loan, C. F. Matrix Computations, North Oxford Academic, Oxford, 1983
[11] TCVN 8244-1:2010 (ISO
3534-1:2006), Thống kê học - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về thống
kê và thuật ngữ dùng trong xác suất
[12] TCVN 8244-2:2010 (ISO
3534-2:2006), Thống kê học - Từ vựng và ký hiệu - Phần 2: Thống kê ứng dụng
[13] ISO/IEC Guide 98-3/Suppl 1,
Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995) - Supplement 1: Propagation of distributions using Monte
Carlo method (Độ không đảm bảo đo - Phần 3: Hướng dẫn trình bày độ
không đảm bảo đo (GUM:1995) - Phần bổ sung 1: Lan truyền phân bố sử dụng phương
pháp Monte Carlo)
[14] TCVN 9598:2013 (ISO 11095:1996),
Hiệu chuẩn tuyến tính sử dụng mẫu chuẩn
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
[16] Kukush, A., and Van Huffel, S. Consistency
of elementwise-weighted total least squares estimator in a multivariate
errors-in-variables model AX = B, Metrika 59, 1 (February 2004), 75-97 (Tính nhất
quán của ước lượng tổng bình phương nhỏ
nhất theo trọng số trong mô hình sai lỗi đa biến)
[17] Mardia, K. V., Kent, J. T., and
Bibby, J. M. Multivariate Analysis, Academic Press, London, 1979 (Phân tích đa
biến)
[18] MATLAB
http://www.mathworks.com/products/matlab/
[19] Migon, H. S. and
Gamerman, D. Statistical Inference: An Integrated Approach, Arnold, London,
1999
[20] Paige, C. C. Fast
numerically stable computations for generalized least squares problems, SIAM J.
Numer. Anal. 16 (1979), 165-171 (Tính toán ổn định số nhanh cho các bài toán
bình phương tối thiểu)
[21] Strang, G., and Borre, K. Linear
Algebra, Geodesy and GPS, Wiley, Wellesley-Cambridge Press, 1997
MỤC LỤC
Lời nói đầu
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
1 Phạm vi áp dụng
2 Tài liệu viện
dẫn
3 Thuật ngữ và
định nghĩa
4 Quy ước và ký
hiệu
5 Các nguyên tắc
hiệu chuẩn đường thẳng
5.1 Khái quát
5.2 Đầu vào để
xác định hàm hiệu chuẩn
5.3 Xác định hàm
hiệu chuẩn
5.4 Xử lý số
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
5.6 Xác nhận giá
trị sử dụng của mô hình
5.7 Sử dụng hàm
hiệu chuẩn
5.8 Xác định đường
thẳng bình phương tối thiểu thông thường khớp nhất với dữ liệu
6 Mô hình dùng
cho độ không đảm bảo gắn với yi
6.1 Khái quát
6.2 Các ước lượng
tham số hiệu chuẩn, độ không đảm bảo chuẩn và hiệp phương sai kèm theo
6.3 Xác nhận giá
trị sử dụng của mô hình
6.4 Tổ chức tính
toán
7 Mô hình độ
không đảm bảo gắn với xi và yi
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
7.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
7.3 Xác nhận giá
trị sử dụng của mô hình
7.4 Tổ chức tính
toán
8 Mô hình độ
không đảm bảo gắn với
xi và yi
và hiệp phương sai gắn với cặp (xi, yi)
8.1 Khái quát
8.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
9 Mô hình độ
không đảm bảo và hiệp phương sai gắn với yi
9.1 Khái quát
9.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
9.4 Tổ chức tính
toán
10 Mô hình độ không đảm
bảo và hiệp phương sai gắn với xi và yi
10.1 Khái quát
10.2 Ước lượng
tham số hiệu chuẩn và độ không đảm bảo chuẩn và hiệp phương sai kèm theo
10.3 Xác nhận giá
trị sử dụng của mô hình
11 Sử dụng hàm
hiệu chuẩn
11.1 Dự đoán
11.2 Đánh giá tiếp
Phụ lục A (tham khảo)
Phép tính ma trận
...
...
...
Bạn phải
đăng nhập hoặc
đăng ký Thành Viên
TVPL Pro để sử dụng được đầy đủ các tiện ích gia tăng liên quan đến nội dung TCVN.
Mọi chi tiết xin liên hệ:
ĐT: (028) 3930 3279 DĐ: 0906 22 99 66
Phụ lục C (tham khảo) Cách tiếp
cận thừa số trực giao để giải quyết bài toán Gauss-Markove tổng quát
Phụ lục D (tham khảo) Quy định về độ
không đảm bảo và hiệp phương sai gắn với x-giá trị và y-giá trị đo được
Phụ lục E (tham khảo) Độ không đảm bảo
đã biết theo hệ
số thang đo
Phụ lục F (tham khảo) Triển khai phần
mềm các thuật toán được mô tả
Phụ lục G (tham khảo) Từ vựng ký hiệu
chính
Thư mục tài liệu tham khảo
